
NIP (model theory)
Encyclopedia
In model theory
, a branch of mathematical logic
, a complete theory T is said to satisfy NIP (or "not the independence property") if none of its formulae satisfy the independence property, that is if none of its formulae can pick out any given subset of an arbitrarily large finite set.
L-theory. An L-formula φ(x,y) is said to have the independence property (with respect to x, y) if in every model M of T there is, for each n = {0,1,…n − 1} < ω, a family of tuple
s b0,…,bn−1 such that for each of the 2n subsets X of n there is a tuple a in M for which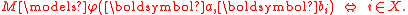
The theory T is said to have the independence property if some formula has the independence property. If no L-formula has the independence property then T is called dependent, or said to satisfy NIP. An L-structure is said to have the independence property (respectively, NIP) if its theory has the independence theory (respectively, NIP). The terminology comes from the notion of independence in the sense of boolean algebras.
In the nomenclature of Vapnik–Chervonenkis theory, we may say that a collection S of subsets of X shatters a set B ⊆ X if every subset of B is of the form B ∩ S for some S ∈ S. Then T has the independence property if in some model M of T there is a definable family (Sa | a∈Mn) ⊆ Mk that shatters arbitrarily large finite subsets of Mk. In other words, (Sa | a∈Mn) has infinite Vapnik–Chervonenkis dimension
.
.
In arithmetic, i.e. the structure (N,+,·), the formula "y divides x" has the independence property. This formula is just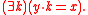
So, for any finite n we take the n 1-tuples bi to be the first n prime number
s, and then for any subset X of {0,1,…n − 1} we let a be the product of those bi such that i is in X. Then bi divides a if and only if i ∈ X.
Every o-minimal theory
satisfies NIP. This fact has had unexpected applications to neural network learning.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a complete theory T is said to satisfy NIP (or "not the independence property") if none of its formulae satisfy the independence property, that is if none of its formulae can pick out any given subset of an arbitrarily large finite set.
Definition
Let T be a completeComplete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
L-theory. An L-formula φ(x,y) is said to have the independence property (with respect to x, y) if in every model M of T there is, for each n = {0,1,…n − 1} < ω, a family of tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s b0,…,bn−1 such that for each of the 2n subsets X of n there is a tuple a in M for which
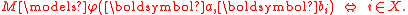
The theory T is said to have the independence property if some formula has the independence property. If no L-formula has the independence property then T is called dependent, or said to satisfy NIP. An L-structure is said to have the independence property (respectively, NIP) if its theory has the independence theory (respectively, NIP). The terminology comes from the notion of independence in the sense of boolean algebras.
In the nomenclature of Vapnik–Chervonenkis theory, we may say that a collection S of subsets of X shatters a set B ⊆ X if every subset of B is of the form B ∩ S for some S ∈ S. Then T has the independence property if in some model M of T there is a definable family (Sa | a∈Mn) ⊆ Mk that shatters arbitrarily large finite subsets of Mk. In other words, (Sa | a∈Mn) has infinite Vapnik–Chervonenkis dimension
VC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
.
Examples
Any complete theory T that has the independence property is unstableStable theory
In model theory, a complete theory is called stable if it does not have too many types. One goal of classification theory is to divide all complete theories into those whose models can be classified and those whose models are too complicated to classify, and to classify all models in the cases...
.
In arithmetic, i.e. the structure (N,+,·), the formula "y divides x" has the independence property. This formula is just
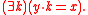
So, for any finite n we take the n 1-tuples bi to be the first n prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, and then for any subset X of {0,1,…n − 1} we let a be the product of those bi such that i is in X. Then bi divides a if and only if i ∈ X.
Every o-minimal theory
O-minimal theory
In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by...
satisfies NIP. This fact has had unexpected applications to neural network learning.

