
Myhill isomorphism theorem
Encyclopedia
In computability theory
the Myhill isomorphism theorem, named after John Myhill
, provides a characterization for two numbering
s to induce the same notion of computability on a set.
s are said to be recursively isomorphic if there is a total computable
bijection
f from the set of natural numbers to itself such that f(A) = B.
A set A of natural numbers is said to be one-one reducible
to a set B if there is a total computable injection f on the natural numbers such that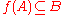 and
and 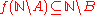 .
.
Myhill's isomorphism theorem states that two sets A and B of natural numbers are recursively isomorphic if and only if A is one-reducible to B and B is one-reducible to A. The theorem is proved by an effective version of the argument used for the Schroeder-Bernstein theorem.
A corollary of Myhill's theorem is that two total numberings
are one-equivalent if and only if they are computably isomorphic.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
the Myhill isomorphism theorem, named after John Myhill
John Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
, provides a characterization for two numbering
Numbering (computability theory)
In computability theory a numbering is the assignment of natural numbers to a set of objects like rational numbers, graphs or words in some language...
s to induce the same notion of computability on a set.
Myhill isomorphism theorem
Sets A and B of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s are said to be recursively isomorphic if there is a total computable
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
f from the set of natural numbers to itself such that f(A) = B.
A set A of natural numbers is said to be one-one reducible
Many-one reduction
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
to a set B if there is a total computable injection f on the natural numbers such that
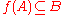 and
and 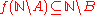 .
.Myhill's isomorphism theorem states that two sets A and B of natural numbers are recursively isomorphic if and only if A is one-reducible to B and B is one-reducible to A. The theorem is proved by an effective version of the argument used for the Schroeder-Bernstein theorem.
A corollary of Myhill's theorem is that two total numberings
Numbering (computability theory)
In computability theory a numbering is the assignment of natural numbers to a set of objects like rational numbers, graphs or words in some language...
are one-equivalent if and only if they are computably isomorphic.

