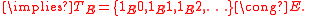Munn semigroup
Encyclopedia
In mathematics, the Munn semigroup
is built from an arbitrary semilattice
.
of E.
2)We define U the uniform relation on E. U: = { (e, f) ∈ E × E : Ee ≃ Ef}
3) For all (e, f) in U, we define Te,f as the set of isomorphisms of Ee onto Ef.
4) Finally, the Munn semigroup of the semilattice
E is defined as: Te := ∐ { Te,f : (e, f) ∈ U }.
The semigroup's operation is the composition of maps. In fact, we can observe that Te ⊆ Ie where Ie is the symmetric inverse semigroup because all isomorphisms are partial one-one maps from subsets of E onto subsets of E.
The idempotents of the Munn semigroup are the identity maps 1Ee.
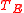is isomorph to E.
Then for all n, En={0,1,2,...,n}
So,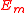
≃
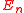⇔ m=n
Hence, U={(n,n) : n ∈ E} =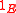
the identity map from E in E. In this case, we say that E is anti-uniform.
Finally,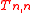
= {
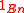} where 
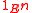is the identity map between En and itself.
Here we can remark that as the theorem stipulated, the semilattice of the idempotents of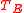
is isomorph to E. In fact, in this example, the whole semigroup is isomorph to E because it is only filled with idempotents.
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
is built from an arbitrary semilattice
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
.Construction's steps
1) For all e in E, we define Ee: = {i ∈ E : i ≤ e} which is an principal idealPrincipal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
of E.
2)We define U the uniform relation on E. U: = { (e, f) ∈ E × E : Ee ≃ Ef}
3) For all (e, f) in U, we define Te,f as the set of isomorphisms of Ee onto Ef.
4) Finally, the Munn semigroup of the semilattice
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
E is defined as: Te := ∐ { Te,f : (e, f) ∈ U }.
The semigroup's operation is the composition of maps. In fact, we can observe that Te ⊆ Ie where Ie is the symmetric inverse semigroup because all isomorphisms are partial one-one maps from subsets of E onto subsets of E.
The idempotents of the Munn semigroup are the identity maps 1Ee.
Theorem
For every semilattice E, the idemtpotents' semilattice of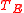 is isomorph to E.Example
Let E={0,1,2,...} a semilattice (0 < 1 < 2 < ...)Then for all n, En={0,1,2,...,n}
So,
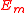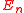≃ ⇔ m=nHence, U={(n,n) : n ∈ E} =
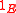the identity map from E in E. In this case, we say that E is anti-uniform.Finally,
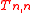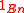= {} where 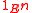is the identity map between En and itself.
Here we can remark that as the theorem stipulated, the semilattice of the idempotents of
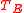is isomorph to E. In fact, in this example, the whole semigroup is isomorph to E because it is only filled with idempotents.