
Multiplier algebra
Encyclopedia
In C*-algebras, the multiplier algebra, denoted by M(A), of a C*-algebra A is a unital C*-algebra which is the largest unital C*-algebra that contains A as an ideal in a "non-degenerate" way. It is the noncommutative generalization of Stone–Čech compactification
. Multiplier algebras were introduced by .
For example, if A is the C*-algebra of compact operators on a separable Hilbert space
, M(A) is B(H), the C*-algebra of all bounded operator
s on H.
Let A be a C*-algebra. Its multiplier algebra M(A) is the C*-algebra satisfying the following universal property
: for all C*-algebra D containing A as an ideal, there exists a unique *-homomorphism φ D → M(A) such that φ extends the identity homomorphism on A and φ(A⊥) = {0}.
Uniqueness up to isomorphism is specified by the universal property. When A is unital, M(A) = A. It also follows from the definition that for any D containing A as an essential ideal, the multiplier algebra M(A) contains D as a C*-subalgebra.
The existence of M(A) can be shown in several ways.
A double centralizer of a C*-algebra A is a pair (L, R) of bounded linear maps on A such that aL(b) = R(a)b for all a and b in A. This implies that ||L|| = ||R||. The set of double centralizers of A can be given a C*-algebra structure. This C*-algebra contains A as an essential ideal and can be identified as the multiplier algebra M(A). For instance, if A is the compact operators K(H) on a separable Hilbert space, then each x ∈ B(H) defines a double centralizer of A by simply multiplication from the left and right.
Alternatively, M(A) can be obtained via representations. The following fact will be needed:
Lemma. If I is an ideal in a C*-algebra B, then any faithful nondegenerate representation π of I can be extended uniquely to B.
Now take any faithful nondegenerate representation πof A on a Hilbert space H. The above lemma, together with the universal property of the multiplier algebra, yields that M(A) is isomorphic to the idealizer
of π(A) in B(H). It is immediate that M(K(H)) = B(H).
Lastly, let E be a Hilbert C*-module and B(E) (resp. K(E)) be the adjointable (resp. compact) operators on E M(A) can be identified via a *-homomorphism of A into B(E). Something similar to the above lemma is true:
Lemma. If I is an ideal in a C*-algebra B, then any faithful nondegenerate *-homomorphism π of I into B(E)can be extended uniquely to B.
Consequently, if π is a faithful nondegenerate *-homomorphism of π into B(E), then M(A) is isomorphic to the idealizer of π(A). For instance, M(K(E)) = B(E) for any Hilbert module E.
The C*-algebra A is isomorphic to the compact operators on the Hilbert module A. Therefore M(A) is the adjointable operators on A.
The resulting topology is called the strict topology on M(A). A is strictly dense in M(A) .
When A is unital, M(A) = A, and the strict topology coincides with the norm topology. For B(H) = M(K(H)), the strict topology is the σ-strong* topology. It follows from above that B(H) is complete in the σ-strong* topology.
, A = C0(X), the commutative C*-algebra of continuous functions with compact support on X. Then M(A) is Cb(X), the continuous bounded functions on X. By the Gelfand-Naimark theorem, one has the isomorphism of C*-algebras

where Y is the spectrum of Cb(X). Y is in fact homeomorphic to the Stone–Čech compactification
of X.
For example, the corona algebra of the algebra of compact operators on a Hilbert space is the Calkin algebra
.
The corona algebra is a non-commutative analogue of the corona set
of a topological space.
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
. Multiplier algebras were introduced by .
For example, if A is the C*-algebra of compact operators on a separable Hilbert space
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
, M(A) is B(H), the C*-algebra of all bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on H.
Definition
An ideal I in a C*-algebra B is said to be essential if I ∩ J is non-trivial for all ideal J. An ideal I is essential if and only if I⊥, the "orthogonal complement" of I in the Hilbert C*-module B is {0}.Let A be a C*-algebra. Its multiplier algebra M(A) is the C*-algebra satisfying the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: for all C*-algebra D containing A as an ideal, there exists a unique *-homomorphism φ D → M(A) such that φ extends the identity homomorphism on A and φ(A⊥) = {0}.
Uniqueness up to isomorphism is specified by the universal property. When A is unital, M(A) = A. It also follows from the definition that for any D containing A as an essential ideal, the multiplier algebra M(A) contains D as a C*-subalgebra.
The existence of M(A) can be shown in several ways.
A double centralizer of a C*-algebra A is a pair (L, R) of bounded linear maps on A such that aL(b) = R(a)b for all a and b in A. This implies that ||L|| = ||R||. The set of double centralizers of A can be given a C*-algebra structure. This C*-algebra contains A as an essential ideal and can be identified as the multiplier algebra M(A). For instance, if A is the compact operators K(H) on a separable Hilbert space, then each x ∈ B(H) defines a double centralizer of A by simply multiplication from the left and right.
Alternatively, M(A) can be obtained via representations. The following fact will be needed:
Lemma. If I is an ideal in a C*-algebra B, then any faithful nondegenerate representation π of I can be extended uniquely to B.
Now take any faithful nondegenerate representation πof A on a Hilbert space H. The above lemma, together with the universal property of the multiplier algebra, yields that M(A) is isomorphic to the idealizer
Idealizer
In mathematics, the idealizer R of an additive subgroup A of a ring R is the largest subring of R that contains A as a two-sided ideal...
of π(A) in B(H). It is immediate that M(K(H)) = B(H).
Lastly, let E be a Hilbert C*-module and B(E) (resp. K(E)) be the adjointable (resp. compact) operators on E M(A) can be identified via a *-homomorphism of A into B(E). Something similar to the above lemma is true:
Lemma. If I is an ideal in a C*-algebra B, then any faithful nondegenerate *-homomorphism π of I into B(E)can be extended uniquely to B.
Consequently, if π is a faithful nondegenerate *-homomorphism of π into B(E), then M(A) is isomorphic to the idealizer of π(A). For instance, M(K(E)) = B(E) for any Hilbert module E.
The C*-algebra A is isomorphic to the compact operators on the Hilbert module A. Therefore M(A) is the adjointable operators on A.
Strict topology
Consider the topology on M(A) specified by the seminorms {la, ra}a ∈ A, where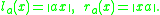
The resulting topology is called the strict topology on M(A). A is strictly dense in M(A) .
When A is unital, M(A) = A, and the strict topology coincides with the norm topology. For B(H) = M(K(H)), the strict topology is the σ-strong* topology. It follows from above that B(H) is complete in the σ-strong* topology.
Commutative case
Let X be a locally compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, A = C0(X), the commutative C*-algebra of continuous functions with compact support on X. Then M(A) is Cb(X), the continuous bounded functions on X. By the Gelfand-Naimark theorem, one has the isomorphism of C*-algebras

where Y is the spectrum of Cb(X). Y is in fact homeomorphic to the Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
of X.
Corona algebra
The corona or corona algebra of A is the quotient M(A)/A.For example, the corona algebra of the algebra of compact operators on a Hilbert space is the Calkin algebra
Calkin algebra
In functional analysis, the Calkin algebra, named after John Wilson Calkin, is the quotient of B, the ring of bounded linear operators on a separable infinite-dimensional Hilbert space H, by the ideal K of compact operators....
.
The corona algebra is a non-commutative analogue of the corona set
Corona set
In mathematics, the corona or corona set of a topological space X is the complement βX\X of the space in its Stone–Čech compactification βX....
of a topological space.

