The missing square puzzle is an optical illusion

Optical illusion

An optical illusion is characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a perception that does not tally with a physical measurement of the stimulus source...

 used in mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

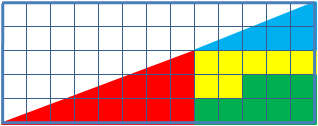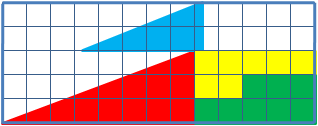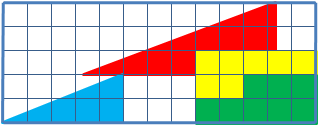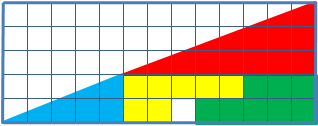
 classes to help students reason about geometrical figures. It depicts two arrangements of shapes, each of which apparently forms a 13×5 right-angled triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

, but one of which has a 1×1 hole in it.

Solution

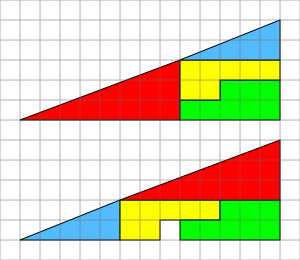
The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, because what would be the hypotenuse

Hypotenuse

In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...

 is bent. In other words, the hypotenuse does not maintain a consistent slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

, even though it may appear that way to the human eye. A true 13 × 5 triangle cannot be created from the given component parts.

The four figures (the yellow, red, blue and green shapes) total 32 units of area, but the triangles are 13 wide and 5 tall, so it seems, that the area should be 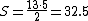units. But the blue triangle has a ratio of 5:2 (=2.5:1), while the red triangle has the ratio 8:3 (≈2.667:1), and these are not the same ratio. So the apparent combined hypotenuse

Hypotenuse

In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...

 in each figure is actually bent.

The amount of bending is around 1/28th of a unit (1.245364267°), which is difficult to see on the diagram of this puzzle. Note the grid point where the red and blue hypotenuses meet, and compare it to the same point on the other figure; the edge is slightly over or under the mark. Overlaying the hypotenuses from both figures results in a very thin parallelogram with the area of exactly one grid square, the same area "missing" from the second figure.
According to Martin Gardner

Martin Gardner

Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...

, the puzzle was invented by a New York City

New York City

New York is the most populous city in the United States and the center of the New York Metropolitan Area, one of the most populous metropolitan areas in the world. New York exerts a significant impact upon global commerce, finance, media, art, fashion, research, technology, education, and...

 amateur magician Paul Curry

Paul Curry

Paul Curry was the vice-president of the Blue Cross Insurance Company of New York, and a famous amateur magician who became well-known in the magic community forinventing highly-original card magic....

 in 1953. The principle of a dissection paradox has however been known since the 1860s.

The integer dimensions of the parts of the puzzle (2, 3, 5, 8, 13) are successive Fibonacci numbers. Many other geometric dissection puzzle

Dissection puzzle

A dissection puzzle, also called a transformation puzzle or Richter Puzzle, is a tiling puzzle where a solver is given a set of pieces that can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of...

s are based on a few simple properties of the famous Fibonacci sequence.

Similar puzzles

A different puzzle of the same kind (depicted in the animation) uses four equal quadrilateral

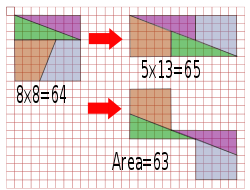
Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

s and a small square, which form a larger square. When the quadrilaterals are rotated about their centers they fill the space of the small square, although the total area of the figure seems unchanged. The apparent paradox is explained by the fact that the side of the new large square is a little smaller than the original one. If is the side of the large square and 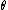is the angle between two opposing sides in each quadrilateral, then the quotient between the two areas is given by 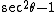. For θ = 5°, this is approximately 1.00765, which corresponds to a difference of about 0.8%.

External links

• A printable Missing Square variant with a video demonstration.
• Curry's Paradox: How Is It Possible? at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Triangles and Paradoxes at archimedes-lab.org
  Archimedes-lab.org
  Archimedes-lab.org is a free and collaborative edutainment website developed and maintained by Gianni A. Sarcone and Marie-Jo Waeber, two authors and writers with more than twenty years of experience in the fields of visual thinking and education...
  
  
• The Triangle Problem or What's Wrong with the Obvious Truth
• Jigsaw Paradox
• The Eleven Holes Puzzle
• Very nice animated Excel workbook of the Missing Square Puzzle
• A video explaining Curry's Paradox and Area by James Stanton