
Minkowski's theorem
Encyclopedia
In mathematics
, Minkowski's theorem is the statement that any convex set
in Rn which is symmetric with respect to the origin and with volume
greater than 2n d(L) contains a non-zero lattice point. The theorem was proved by Hermann Minkowski
in 1889 and became the foundation of the branch of number theory
called the geometry of numbers
.
of determinant
d(L) in the n-dimensional real vector space
Rn and S is a convex subset
of Rn that is symmetric with respect to the origin, meaning that if x is in S then −x is also in S.
Minkowski's theorem states that if the volume of S is strictly greater than 2n d(L), then S must contain at least one lattice point other than the origin.
coefficients; its determinant is 1. For n = 2 the theorem claims that a convex figure in the plane symmetric about the origin
and with area
greater than 4 encloses at least one lattice point in addition to the origin. The area bound is sharp: if S is the interior of the square with vertices (±1, ±1) then S is symmetric and convex, has area 4, but the only lattice point it contains is the origin. This observation generalizes to every dimension n.
Consider the map . Intuitively, this map cuts the plane into 2 by 2 squares, then stacks the squares on top of each other. Clearly
. Intuitively, this map cuts the plane into 2 by 2 squares, then stacks the squares on top of each other. Clearly 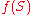 has area ≤ 4. Suppose f were injective, which means the pieces of S cut out by the squares stack up in a non-overlapping way. Since f is locally area-preserving, this non-overlapping property would make it area-preserving for all of S, so the area of f(S) would be the same as that of S, which is greater than 4. That is not the case, so f is not injective, and
has area ≤ 4. Suppose f were injective, which means the pieces of S cut out by the squares stack up in a non-overlapping way. Since f is locally area-preserving, this non-overlapping property would make it area-preserving for all of S, so the area of f(S) would be the same as that of S, which is greater than 4. That is not the case, so f is not injective, and 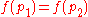 for some pair of points
for some pair of points 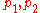 in S. Moreover, we know from the definition of f that
in S. Moreover, we know from the definition of f that  for some integers i and j, where i and j are not both zero.
for some integers i and j, where i and j are not both zero.
Then since S is symmetric about the origin, is also a point in S. Since S is convex, the line segment between
is also a point in S. Since S is convex, the line segment between  and
and  lies entirely in S, and in particular the midpoint of that segment lies in S. In other words,
lies entirely in S, and in particular the midpoint of that segment lies in S. In other words,
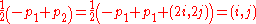
lies in S. (i,j) is a lattice point, and is not the origin since i and j are not both zero, and so we have found the point we're looking for.
of a number field K contains an integral ideal of norm
not exceeding a certain bound, depending on K, called Minkowski's bound
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Minkowski's theorem is the statement that any convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in Rn which is symmetric with respect to the origin and with volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
greater than 2n d(L) contains a non-zero lattice point. The theorem was proved by Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
in 1889 and became the foundation of the branch of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
called the geometry of numbers
Geometry of numbers
In number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
.
Formulation
Suppose that L is a latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
of determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
d(L) in the n-dimensional real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Rn and S is a convex subset
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
of Rn that is symmetric with respect to the origin, meaning that if x is in S then −x is also in S.
Minkowski's theorem states that if the volume of S is strictly greater than 2n d(L), then S must contain at least one lattice point other than the origin.
Example
The simplest example of a lattice is the set Zn of all points with integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients; its determinant is 1. For n = 2 the theorem claims that a convex figure in the plane symmetric about the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
and with area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
greater than 4 encloses at least one lattice point in addition to the origin. The area bound is sharp: if S is the interior of the square with vertices (±1, ±1) then S is symmetric and convex, has area 4, but the only lattice point it contains is the origin. This observation generalizes to every dimension n.
Proof
The following argument proves Minkowski's theorem for the special case of L=Z2. It can be generalized to arbitrary lattices in arbitrary dimensions.Consider the map
 . Intuitively, this map cuts the plane into 2 by 2 squares, then stacks the squares on top of each other. Clearly
. Intuitively, this map cuts the plane into 2 by 2 squares, then stacks the squares on top of each other. Clearly 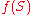 has area ≤ 4. Suppose f were injective, which means the pieces of S cut out by the squares stack up in a non-overlapping way. Since f is locally area-preserving, this non-overlapping property would make it area-preserving for all of S, so the area of f(S) would be the same as that of S, which is greater than 4. That is not the case, so f is not injective, and
has area ≤ 4. Suppose f were injective, which means the pieces of S cut out by the squares stack up in a non-overlapping way. Since f is locally area-preserving, this non-overlapping property would make it area-preserving for all of S, so the area of f(S) would be the same as that of S, which is greater than 4. That is not the case, so f is not injective, and 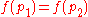 for some pair of points
for some pair of points 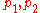 in S. Moreover, we know from the definition of f that
in S. Moreover, we know from the definition of f that  for some integers i and j, where i and j are not both zero.
for some integers i and j, where i and j are not both zero.Then since S is symmetric about the origin,
 is also a point in S. Since S is convex, the line segment between
is also a point in S. Since S is convex, the line segment between  and
and  lies entirely in S, and in particular the midpoint of that segment lies in S. In other words,
lies entirely in S, and in particular the midpoint of that segment lies in S. In other words,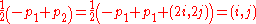
lies in S. (i,j) is a lattice point, and is not the origin since i and j are not both zero, and so we have found the point we're looking for.
Applications
A corollary of this theorem is the fact that every class in the ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of a number field K contains an integral ideal of norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
not exceeding a certain bound, depending on K, called Minkowski's bound
Minkowski's bound
In algebraic number theory, Minkowski's bound gives an upper bound of the norm of ideals to be checked in order to determine the class number of a number field K...
.

