Mexican hat wavelet
Encyclopedia
In mathematics
and numerical analysis
, the Mexican hat wavelet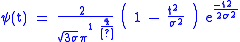
is the negative normalized
second derivative
of a Gaussian function, i.e., up to scale and normalization, the second Hermite function. It is a special case of the family of continuous wavelet
s (wavelet
s used in a continuous wavelet transform
) known as Hermitian wavelets. It is usually only referred to as the "Mexican hat" in the Americas, due to cultural association; see "sombrero
". In technical nomenclature this function is known as the Ricker wavelet, where it is frequently employed to model seismic data.
The multidimensional generalization of this wavelet is called the Laplacian of Gaussian function. In practice, this wavelet is sometimes approximated by the difference of Gaussians
function, because it is separable and can therefore save considerable computation time in two or more dimensions. The scale normalised Laplacian (in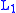
-norm) is frequently used as a blob detector
and for automatic scale selection in computer vision
applications; see Laplacian of Gaussian and scale-space. The Mexican hat wavelet can also be approximated by derivative
s of Cardinal B-Splines
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Mexican hat wavelet
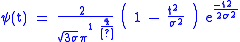
is the negative normalized
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
second derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a Gaussian function, i.e., up to scale and normalization, the second Hermite function. It is a special case of the family of continuous wavelet
Continuous wavelet
In numerical analysis, continuous wavelets are functions used by the continuous wavelet transform. These functions are defined as analytical expressions, as functions either of time or of frequency....
s (wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
s used in a continuous wavelet transform
Continuous wavelet transform
A continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization...
) known as Hermitian wavelets. It is usually only referred to as the "Mexican hat" in the Americas, due to cultural association; see "sombrero
Sombrero
Sombrero in English refers to a type of wide-brimmed hat originating in Mexico. In Spanish, however, it is the generic word for "hat", which originates from "sombra", meaning "shade"....
". In technical nomenclature this function is known as the Ricker wavelet, where it is frequently employed to model seismic data.
The multidimensional generalization of this wavelet is called the Laplacian of Gaussian function. In practice, this wavelet is sometimes approximated by the difference of Gaussians
Difference of Gaussians
In computer vision, Difference of Gaussians is a grayscale image enhancement algorithm that involves the subtraction of one blurred version of an original grayscale image from another, less blurred version of the original. The blurred images are obtained by convolving the original grayscale image...
function, because it is separable and can therefore save considerable computation time in two or more dimensions. The scale normalised Laplacian (in
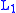-norm) is frequently used as a blob detectorBlob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
and for automatic scale selection in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
applications; see Laplacian of Gaussian and scale-space. The Mexican hat wavelet can also be approximated by derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of Cardinal B-Splines