McCarthy 91 function
Encyclopedia
The McCarthy 91 function is a recursive function
, defined by computer scientist
John McCarthy
as a test case for formal verification
within computer science
.
The McCarthy 91 function is defined as
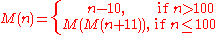
The results of evaluating the function are given by M(n) = 91 for all integer arguments n ≤ 100, and M(n) = n − 10 for n ≥ 101.
, Amir Pnueli and John McCarthy
in 1970. These papers represented early developments towards the application of formal methods
to program verification
. The 91 function was chosen for having a complex recursion pattern (contrasted with simple patterns, such as defining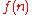
by means of 
). The example was popularized by Manna's book, Mathematical Theory of Computation (1974). As the field of Formal Methods advanced, this example appeared repeatedly in the research literature.
In particular, it is viewed as a "challenge problem" for automated program verification.
Often, it is easier to reason about non-recursive computation. As one of the examples used to demonstrate such reasoning, Manna's book includes a non-recursive algorithm that simulates the original (recursive) 91 function. Many of the papers that report an "automated verification" (or termination proof) of the 91 function only handle the non-recursive version.
A formal derivation of the non-recursive version from the recursive one was given in a 1980 article by Mitchell Wand
, based on the use of continuation
s.
M(99) = M(M(110)) since 99 ≤ 100
= M(100) since 110 > 100
= M(M(111)) since 100 ≤ 100
= M(101) since 111 > 100
= 91 since 101 > 100
Example B:
M(87) = M(M(98))
= M(M(M(109)))
= M(M(99))
= M(M(M(110)))
= M(M(100))
= M(M(M(111)))
= M(M(101))
= M(91)
= M(M(102))
= M(92)
= M(M(103))
= M(93)
.... Pattern continues
= M(99)
(same as example A)
= 91
, the language he invented:
(defun mc91 (n)
(cond ((<= n 100) (mc91 (mc91 (+ n 11))))
(t (- n 10))))
Here is an implementation of the non-recursive algorithm in C
:
int mccarthy(int n)
{
int c;
for (c = 1; c != 0; ) {
if (n > 100) {
n = n - 10;
c--;
} else {
n = n + 11;
c++;
}
}
return n;
}
For 90 ≤ n < 101,
M(n) = M(M(n + 11))
= M(n + 11 - 10), where n + 11 >= 101 since n >= 90
= M(n + 1)
So M(n) = 91 for 90 ≤ n < 101.
We can use this as a base case for induction on blocks of 11 numbers, like so:
Assume that M(n) = 91 for a ≤ n < a + 11.
Then, for any n such that a - 11 ≤ n < a,
M(n) = M(M(n + 11))
= M(91), by hypothesis, since a ≤ n + 11 < a + 11
= 91, by the base case.
Now by induction M(n) = 91 for any n in such a block. There are no holes between the blocks, so M(n) = 91 for n < 101. We can also add n = 101 as a special case.
generalized the 91 function to include additional parameters. John Cowles developed a formal proof that Knuth's generalized function was total, using the ACL2 theorem prover.
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
, defined by computer scientist
Computer scientist
A computer scientist is a scientist who has acquired knowledge of computer science, the study of the theoretical foundations of information and computation and their application in computer systems....
John McCarthy
John McCarthy (computer scientist)
John McCarthy was an American computer scientist and cognitive scientist. He coined the term "artificial intelligence" , invented the Lisp programming language and was highly influential in the early development of AI.McCarthy also influenced other areas of computing such as time sharing systems...
as a test case for formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
within computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
The McCarthy 91 function is defined as
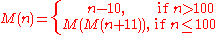
The results of evaluating the function are given by M(n) = 91 for all integer arguments n ≤ 100, and M(n) = n − 10 for n ≥ 101.
History
The 91 function was introduced in papers published by Zohar MannaZohar Manna
Zohar Manna is a professor of computer science at Stanford University. He is the author of The Mathematical Theory of Computation , one of the first texts to provide extensive coverage of the mathematical concepts behind computer programming.With Amir Pnueli, he co-authored an unfinished trilogy...
, Amir Pnueli and John McCarthy
John McCarthy (computer scientist)
John McCarthy was an American computer scientist and cognitive scientist. He coined the term "artificial intelligence" , invented the Lisp programming language and was highly influential in the early development of AI.McCarthy also influenced other areas of computing such as time sharing systems...
in 1970. These papers represented early developments towards the application of formal methods
Formal methods
In computer science and software engineering, formal methods are a particular kind of mathematically-based techniques for the specification, development and verification of software and hardware systems...
to program verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
. The 91 function was chosen for having a complex recursion pattern (contrasted with simple patterns, such as defining
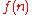by means of ). The example was popularized by Manna's book, Mathematical Theory of Computation (1974). As the field of Formal Methods advanced, this example appeared repeatedly in the research literature.In particular, it is viewed as a "challenge problem" for automated program verification.
Often, it is easier to reason about non-recursive computation. As one of the examples used to demonstrate such reasoning, Manna's book includes a non-recursive algorithm that simulates the original (recursive) 91 function. Many of the papers that report an "automated verification" (or termination proof) of the 91 function only handle the non-recursive version.
A formal derivation of the non-recursive version from the recursive one was given in a 1980 article by Mitchell Wand
Mitchell Wand
Mitchell Wand is a Computer Science professor at Northeastern University. He received his Ph.D. degrees from MIT. His research has centred on programming languages and is a member of the Northeastern Programming Research Lab. He is also the co-author of Essentials of Programming Languages.-External...
, based on the use of continuation
Continuation
In computer science and programming, a continuation is an abstract representation of the control state of a computer program. A continuation reifies the program control state, i.e...
s.
Examples
Example A:M(99) = M(M(110)) since 99 ≤ 100
= M(100) since 110 > 100
= M(M(111)) since 100 ≤ 100
= M(101) since 111 > 100
= 91 since 101 > 100
Example B:
M(87) = M(M(98))
= M(M(M(109)))
= M(M(99))
= M(M(M(110)))
= M(M(100))
= M(M(M(111)))
= M(M(101))
= M(91)
= M(M(102))
= M(92)
= M(M(103))
= M(93)
.... Pattern continues
= M(99)
(same as example A)
= 91
Code
Here is how John McCarthy may have written this function in LispLisp programming language
Lisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
, the language he invented:
(defun mc91 (n)
(cond ((<= n 100) (mc91 (mc91 (+ n 11))))
(t (- n 10))))
Here is an implementation of the non-recursive algorithm in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
:
int mccarthy(int n)
{
int c;
for (c = 1; c != 0; ) {
if (n > 100) {
n = n - 10;
c--;
} else {
n = n + 11;
c++;
}
}
return n;
}
Proof
Here is a proof that the function behaves as expected.For 90 ≤ n < 101,
M(n) = M(M(n + 11))
= M(n + 11 - 10), where n + 11 >= 101 since n >= 90
= M(n + 1)
So M(n) = 91 for 90 ≤ n < 101.
We can use this as a base case for induction on blocks of 11 numbers, like so:
Assume that M(n) = 91 for a ≤ n < a + 11.
Then, for any n such that a - 11 ≤ n < a,
M(n) = M(M(n + 11))
= M(91), by hypothesis, since a ≤ n + 11 < a + 11
= 91, by the base case.
Now by induction M(n) = 91 for any n in such a block. There are no holes between the blocks, so M(n) = 91 for n < 101. We can also add n = 101 as a special case.
Knuth's generalization
Donald KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
generalized the 91 function to include additional parameters. John Cowles developed a formal proof that Knuth's generalized function was total, using the ACL2 theorem prover.