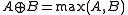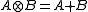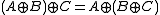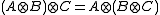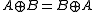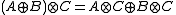Max-plus algebra
Encyclopedia
A max-plus algebra is an algebra
over the real number
s with maximum and addition as the two binary operations.
It can be used appropriately to determine marking times within a given Petri net
and a vector filled with marking state at the beginning.
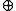) and addition (plus operator 
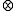) for this scalars are defined as
Watch: Max-operator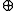
can easily be confused with the addition operation. All 
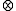- operations have a higher precedence
than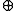
- operations.
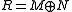- operation, the elements of the resulting matrix R (row i, column j) have to be set up by the maximum operation of both corresponding elements of the matrices M and N:
The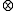
- operation is similar to algorithm of Matrix multiplication
, however, every "+" calculation has to be substituted by a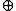
- operation, every "
" calculation by a 
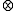- operation.
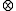which means "never before", the ε-element has been established by ε
. According to the idea of infinity, the following equations can be found:
To point the zero number out, the element e was defined by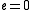
. Therefore:
Obviously, ε is the neutral element for the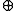
- operation as well as e is for the 
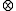- operation
Note: In general, A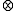
B = B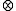 
A does not hold, for example in the case of matrix operations.
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with maximum and addition as the two binary operations.
It can be used appropriately to determine marking times within a given Petri net
Petri net
A Petri net is one of several mathematical modeling languages for the description of distributed systems. A Petri net is a directed bipartite graph, in which the nodes represent transitions and places...
and a vector filled with marking state at the beginning.
Scalar operations
Let A and B be scalars. Then the operations maximum (implied by the max operator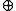) and addition (plus operator 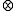) for this scalars are defined as
Watch: Max-operator
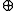can easily be confused with the addition operation. All 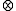- operations have a higher precedenceOrder of operations
In mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
than
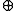- operations.Matrix operations
Max-Plus algebra can be used for matrix operands M, N likewise. To perform the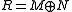 - operation, the elements of the resulting matrix R (row i, column j) have to be set up by the maximum operation of both corresponding elements of the matrices M and N:- Rij = M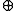ij
Nij
The
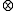- operation is similar to algorithm of Matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, however, every "+" calculation has to be substituted by a
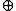- operation, every "" calculation by a 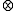- operation.Useful enhancement elements
In order to handle marking times like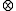 which means "never before", the ε-element has been established by ε. According to the idea of infinity, the following equations can be found:- ε
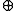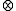A = A - ε
A = ε
To point the zero number out, the element e was defined by
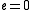. Therefore:- e
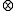A = A
Obviously, ε is the neutral element for the
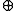- operation as well as e is for the 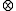- operationAlgebra properties
- associativity:
- commutativity :
- distributivity:
Note: In general, A
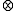B = B 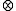A does not hold, for example in the case of matrix operations.