Matérn covariance function
Encyclopedia
In statistics
, the Matérn covariance (named after the Swedish forestry statistician Bertil Matérn) is a covariance function
used in spatial statistics, geostatistics
, machine learning
, image analysis, and other applications of multivariate statistical analysis on metric space
s. It is commonly used to define the statistical covariance between measurements made at two points that are d units distant from each other. Since the covariance only depends on distances between points, it is stationary
. If the distance is Euclidean distance
, the Matérn covariance is also isotropic.
The Matérn covariance between two points separated by d distance units is given by
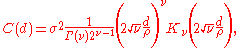
where Γ is the gamma function
, Kν is the modified Bessel function
of the second kind, and ρ and ν are non-negative parameter
s of the covariance.
A Gaussian process
with Matérn covariance has sample paths that are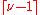
times differentiable. As 
, the Matérn covariance converges to the squared exponential covariance function
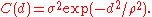
When ν = 0.5, the Matérn covariance is identical to the exponential covariance function.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Matérn covariance (named after the Swedish forestry statistician Bertil Matérn) is a covariance function
Covariance function
In probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
used in spatial statistics, geostatistics
Geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology,...
, machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, image analysis, and other applications of multivariate statistical analysis on metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. It is commonly used to define the statistical covariance between measurements made at two points that are d units distant from each other. Since the covariance only depends on distances between points, it is stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
. If the distance is Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, the Matérn covariance is also isotropic.
The Matérn covariance between two points separated by d distance units is given by
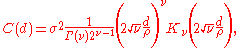
where Γ is the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, Kν is the modified Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the second kind, and ρ and ν are non-negative parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s of the covariance.
A Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
with Matérn covariance has sample paths that are
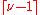times differentiable. As , the Matérn covariance converges to the squared exponential covariance function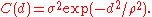When ν = 0.5, the Matérn covariance is identical to the exponential covariance function.