
Mass point geometry
Encyclopedia
Mass point geometry, colloquially known as mass points, is a geometry problem-solving technique which applies the physical principle of the center of mass
to geometry problems involving triangles and intersecting cevian
s. All problems that can be solved using mass point geometry can also be solved using either similar triangles, vectors, or area ratios, but mass point geometry is far quicker than those methods and thus is used more often on math competitions in which time is an important factor. Though modern mass point geometry was developed in the 1960s by New York high school students, the concept has been found to have been used as early as 1827 by August Ferdinand Möbius
in his theory of homogenous coordinates.
in addition to cevians. Any vertex that is on both sides the transversal crosses will have a split mass. A point with a split mass may be treated as a normal mass point, except that it has three masses: one used for each of the two sides it is on, and one that is the sum of the other two split masses and is used for any cevians it may have. See Problem Two for an example.
 ,
,  is on
is on 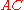 so that
so that 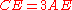 and
and  is on
is on  so that
so that 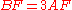 . If
. If  and
and  intersect at
intersect at  and line
and line  intersects
intersects  at
at  , compute
, compute  and
and  .
.
Solution. We may arbitrarily assign the mass of point to be
to be  . By ratios of lengths, the masses at
. By ratios of lengths, the masses at  and
and  must both be
must both be 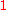 . By summing masses, the masses at
. By summing masses, the masses at  and
and  are both
are both  . Furthermore, the mass at
. Furthermore, the mass at  is
is  , making the mass at
, making the mass at  have to be
have to be  Therefore
Therefore 
 and
and  . See diagram at right.
. See diagram at right.
 ,
,  ,
,  , and
, and  are on
are on  ,
,  , and
, and  respectively so that
respectively so that 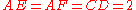 ,
,  , and
, and 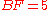 . If
. If  and
and 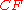 intersect at
intersect at  , compute
, compute 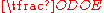 and
and  .
.
Solution. As this problem involves a transversal, we must use split masses on point . We may arbitrarily assign the mass of point
. We may arbitrarily assign the mass of point  to be
to be  . By ratios of lengths, the mass at
. By ratios of lengths, the mass at  must be
must be  and the mass at
and the mass at  is split
is split  towards
towards  and
and  towards
towards  . By summing masses, we get the masses at
. By summing masses, we get the masses at  ,
,  , and
, and  to be
to be  ,
, 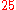 , and
, and  respectively. Therefore
respectively. Therefore  and
and  .
.
 , points
, points  and
and  are on sides
are on sides  and
and  respectively, and points
respectively, and points  and
and  are on side
are on side  with
with  between
between  and
and  .
.  intersects
intersects  at point
at point  and
and  intersects
intersects  at point
at point  . If
. If  ,
,  , and
, and  , compute
, compute  .
.
Solution. This problem involves two central intersection points, and
and 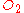 , so we must use multiple systems.
, so we must use multiple systems.
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
to geometry problems involving triangles and intersecting cevian
Cevian
In geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians...
s. All problems that can be solved using mass point geometry can also be solved using either similar triangles, vectors, or area ratios, but mass point geometry is far quicker than those methods and thus is used more often on math competitions in which time is an important factor. Though modern mass point geometry was developed in the 1960s by New York high school students, the concept has been found to have been used as early as 1827 by August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
in his theory of homogenous coordinates.
Definitions
The theory of mass points is rigorously defined according to the following definitions:- Mass Point - A mass point is a pair
 , also written as
, also written as  , including a mass,
, including a mass,  , and an ordinary point,
, and an ordinary point,  on a plane.
on a plane. - Coincidence - We say that two points
 and
and  coincide if and only if
coincide if and only if  and
and  .
. - Addition - The sum of two mass points
 and
and  has mass
has mass  and point
and point  where
where  is the point on
is the point on  such that
such that  . In other words,
. In other words,  is the fulcrum point that perfectly balances the points
is the fulcrum point that perfectly balances the points 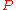 and
and  . An example of mass point addition is shown at right. Mass point addition is closedClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
. An example of mass point addition is shown at right. Mass point addition is closedClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
, idempotent, commutative, and associative. - Scalar Multiplication - Given a mass point
 and a positive real scalar
and a positive real scalar 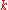 , we define multiplication to be
, we define multiplication to be  . Mass point scalar multiplication is distributive over mass point addition.
. Mass point scalar multiplication is distributive over mass point addition.
Concurrent cevians
The method of using mass point geometry to solve problems with concurrent cevians is quite simple, and does not require much knowledge of the theory behind it. To begin with, a single point is assigned an arbitrary mass, usually one that allows the other masses in the problem to be integral. The masses at the other points are calculated so that the feet of cevians are the sum of the two mass point vertices they are between. For each cevian, the point of concurrency is the sum of the mass point vertex and foot of that cevian. Each length ratio may then be calculated from the masses at the points. See Problem One for an example.Splitting masses
Splitting masses is the slightly more complicated method necessary when a problem contains transversalsTransversal (geometry)
In geometry, a transversal is a line that passes through two or more other lines in the same plane at different points. When the lines are parallel, as is often the case, a transversal produces several congruent and several supplementary angles...
in addition to cevians. Any vertex that is on both sides the transversal crosses will have a split mass. A point with a split mass may be treated as a normal mass point, except that it has three masses: one used for each of the two sides it is on, and one that is the sum of the other two split masses and is used for any cevians it may have. See Problem Two for an example.
Other methods
- Routh's theorem - Many problems involving triangles with cevians will ask for areas, and mass points does not provide a method for calculating areas. However, Routh's theoremRouth's theoremIn geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians...
, which goes hand in hand with mass points, uses ratios of lengths to calculate the ratio of areas between a triangle and a triangle formed by three cevians. - Special cevians - When given cevians with special properties, like an angle bisector or an altitudeAltitudeAltitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
, other theorems may be used alongside mass point geometry that determine length ratios. One very common theorem used likewise is the angle bisector theoremAngle bisector theoremIn geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.Consider a triangle...
. - Stewart's theorem - When asked not for the ratios of lengths but for the actual lengths themselves, Stewart's theoremStewart's theoremIn geometry, Stewart's theorem yields a relation between a lengths of the sides of the triangle and the length of a cevian of the triangle. Its name is in honor of the Scottish mathematician Matthew Stewart who published the theorem in 1746.- Theorem :...
may be used to determine the length of the entire segment, and then mass points may be used to determine the ratios and therefore the necessary lengths of parts of segments. - Higher dimensions - The methods involved in mass point geometry are not limited to two dimensions; the same methods may be used in problems involving tetrahedra, or even higher-dimensional shapes, though it is rare that a problem involving four or more dimensions will require use of mass points.
Examples
Problem One
Problem. In triangle ,
,  is on
is on 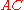 so that
so that 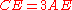 and
and  is on
is on  so that
so that 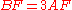 . If
. If  and
and  intersect at
intersect at  and line
and line  intersects
intersects  at
at  , compute
, compute  and
and  .
.Solution. We may arbitrarily assign the mass of point
 to be
to be  . By ratios of lengths, the masses at
. By ratios of lengths, the masses at  and
and  must both be
must both be 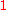 . By summing masses, the masses at
. By summing masses, the masses at  and
and  are both
are both  . Furthermore, the mass at
. Furthermore, the mass at  is
is  , making the mass at
, making the mass at  have to be
have to be  Therefore
Therefore 
 and
and  . See diagram at right.
. See diagram at right.Problem Two
Problem. In triangle ,
,  ,
,  , and
, and  are on
are on  ,
,  , and
, and  respectively so that
respectively so that 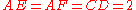 ,
,  , and
, and 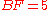 . If
. If  and
and 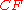 intersect at
intersect at  , compute
, compute 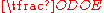 and
and  .
.Solution. As this problem involves a transversal, we must use split masses on point
 . We may arbitrarily assign the mass of point
. We may arbitrarily assign the mass of point  to be
to be  . By ratios of lengths, the mass at
. By ratios of lengths, the mass at  must be
must be  and the mass at
and the mass at  is split
is split  towards
towards  and
and  towards
towards  . By summing masses, we get the masses at
. By summing masses, we get the masses at  ,
,  , and
, and  to be
to be  ,
, 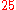 , and
, and  respectively. Therefore
respectively. Therefore  and
and  .
.Problem Three
Problem. In triangle , points
, points  and
and  are on sides
are on sides  and
and  respectively, and points
respectively, and points  and
and  are on side
are on side  with
with  between
between  and
and  .
.  intersects
intersects  at point
at point  and
and  intersects
intersects  at point
at point  . If
. If  ,
,  , and
, and  , compute
, compute  .
.Solution. This problem involves two central intersection points,
 and
and 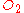 , so we must use multiple systems.
, so we must use multiple systems.- System One. For the first system, we will choose
 as our central point, and we may therefore ignore segment
as our central point, and we may therefore ignore segment  and points
and points  ,
,  , and
, and 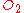 . We may arbitrarily assign the mass at
. We may arbitrarily assign the mass at  to be
to be  , and by ratios of lengths the masses at
, and by ratios of lengths the masses at  and
and  are
are  and
and  respectively. By summing masses, we get the masses at
respectively. By summing masses, we get the masses at  ,
,  , and
, and  to be 10, 9, and 13 respectively. Therefore,
to be 10, 9, and 13 respectively. Therefore,  and
and  .
.
- System Two. For the second system, we will choose
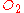 as our central point, and we may therefore ignore segment
as our central point, and we may therefore ignore segment 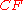 and points
and points  and
and  . As this system involves a transversal, we must use split masses on point
. As this system involves a transversal, we must use split masses on point  . We may arbitrarily assign the mass at
. We may arbitrarily assign the mass at  to be
to be  , and by ratios of lengths, the mass at
, and by ratios of lengths, the mass at  is
is  and the mass at
and the mass at  is split
is split  towards
towards  and 2 towards
and 2 towards  . By summing masses, we get the masses at
. By summing masses, we get the masses at  ,
,  , and
, and  to be 4, 6, and 10 respectively. Therefore,
to be 4, 6, and 10 respectively. Therefore,  and
and  .
.
- Original System. We now know all the ratios necessary to put together the ratio we are asked for. The final answer may be found as follows:
See also
- CevianCevianIn geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians...
- Ceva's theoremCeva's theoremCeva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O to meet opposite sides at D, E and F respectively...
- Menelaus's theorem
- Stewart's theoremStewart's theoremIn geometry, Stewart's theorem yields a relation between a lengths of the sides of the triangle and the length of a cevian of the triangle. Its name is in honor of the Scottish mathematician Matthew Stewart who published the theorem in 1746.- Theorem :...
- Angle bisector theoremAngle bisector theoremIn geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.Consider a triangle...
- Routh's theoremRouth's theoremIn geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians...
- Barycentric coordinatesBarycentric coordinates (mathematics)In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...


