
Magnitude condition
Encyclopedia
The magnitude condition is a constraint that is satisfied by the locus of points in the s-plane on which closed-loop poles of a system reside. In combination with the angle condition, these two mathematical expressions fully determine the root locus
.
Let the characteristic equation
of a system be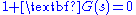 , where
, where 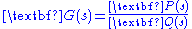 . Rewriting the equation in polar form is useful.
. Rewriting the equation in polar form is useful.
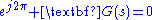
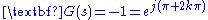 where
where
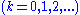 are the only solutions to this equation. Rewriting
are the only solutions to this equation. Rewriting 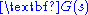 in factored form,
in factored form,
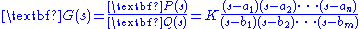 ,
,
and representing each factor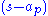 and
and 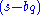 by their vector equivalents,
by their vector equivalents, 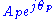 and
and 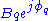 , respectively,
, respectively, 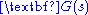 may be rewritten.
may be rewritten.
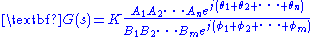
Simplifying the characteristic equation,
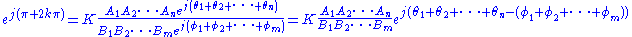 ,
,
from which we derive the magnitude condition:
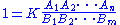 .
.
The angle condition is derived similarly.
Root locus
Root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly the gain of a feedback system. This is a technique used in the field of control systems developed by Walter R...
.
Let the characteristic equation
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
of a system be
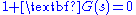 , where
, where 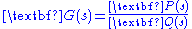 . Rewriting the equation in polar form is useful.
. Rewriting the equation in polar form is useful.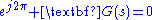
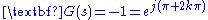 where
where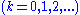 are the only solutions to this equation. Rewriting
are the only solutions to this equation. Rewriting 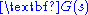 in factored form,
in factored form,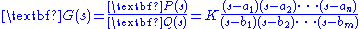 ,
,and representing each factor
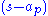 and
and 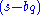 by their vector equivalents,
by their vector equivalents, 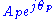 and
and 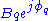 , respectively,
, respectively, 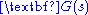 may be rewritten.
may be rewritten.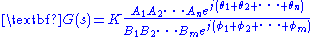
Simplifying the characteristic equation,
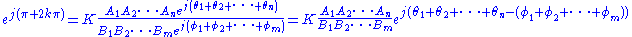 ,
,from which we derive the magnitude condition:
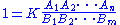 .
.The angle condition is derived similarly.

