Magic circles were invented by the Song Dynasty

Song Dynasty

The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...

 (960–1279) Chinese

China

Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...

 mathematician Yang Hui

Yang Hui

Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...

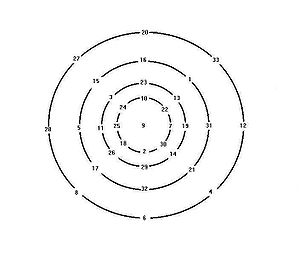
(c. 1238–1298). It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical. One of his magic circles was constructed from 33 natural numbers from 1 to 33 arranged on four circles , with 9 at the center.

Yang Hui magic circles

Yang Hui's magic circle has the following properties

• The sum of the numbers on four diameters = 147，
  • 28 + 5 + 11 + 25 + 9 + 7 + 19 + 31 + 12 = 147
• The sum of 8 numbers plus 9 at the center =147;
  • 28 + 27 + 20 + 33 + 12 + 4 + 6 + 8 + 9 = 147
• The sum of eight radius without 9 =magic number 69: such as 27 + 15 + 3 + 24 = 69
• The sum of all numbers on each circle (not including 9) = 2 × 69
• There exist 8 semicircles, where the sum of numbers = magic number 69; there are 16 line segments(semi circles and radii) with magic number 69, more than a 6 order magic square with only 12 magic numbers.

Yang Hui's magic square was published in his Xugu Zhaiqi Suanfa《續古摘奇算法》 (Sequel to Excerpts of Mathematical Wonders) of 1275.

Ding Yidong magic circles

Ding Yidong was a mathematician contemporary with Yang Hui, in his 6th order magic circle
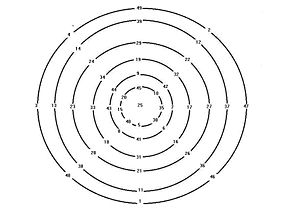
with 6 rings, the 5 out rings have connection with a 3rd order magic square: the unit number of the 8 numbers on any ring form a 3rd order magic square.

4	9	2
3	5	7
8	1	6

Method of construction:

Let radial group 1 =1,11,21,31,41

Let radial group 2=2,12,22,32,42

Let radial group 3=3,13,23,33,43

Let radial group 4=4,14,24,34,44

Let radial group 6=6,16,26,36,46

Let radial group 7=7,17,27,37,47

Let radial group 8=8,18,28,38,48

Let radial group 9=9,19,29,39,49

Let center group =5,15,25,35,45

Arrange group 1,2,3,4,6,7,9 radially such that

• each number occupies one position on circle
• alternate the direction such that one radial has smallest number at the outside, the adjacent radial has largest number outside.
• Each group occupies the radial position corresponding to the number on the Luoshu magic square, i.e., group 1 at 1 position, group 2 at

2 position etc.

• Finally arrange center group at the center circle, such that

number 5 on group 1 radial

number 10 on group 2 radial

number 15 on group 3 radial

...

number 45 on group 9 radial