Machine that always halts
Encyclopedia
In computability theory
, a machine that always halts—also called a decider (Sipser, 1996) or a total Turing machine (Kozen, 1997)—is a Turing machine
that halts for every input.
Because it always halts, the machine is able to decide whether a given string is a member of a formal language
. The class of languages which can be decided by such machines is exactly the set of recursive language
s. However, due to the Halting Problem
, determining whether an arbitrary Turing machine
halts on an arbitrary input is itself an undecidable
decision problem
.
capabilities so that no input will ever cause the machine to enter an infinite loop
. As a trivial example, a machine implementing a finitary decision tree
will always halt.
It is not required that the machine be entirely free of looping capabilities, however, to guarantee halting. If we restrict loops to be of a predictably finite size (not unlike the FOR loop in BASIC
), we can express all of the primitive recursive functions (Meyer and Ritchie, 1967). An example of such a machine is provided by the toy programming language PL-{GOTO} of Brainerd and Landweber (1974).
We can further define a programming language in which we can ensure that even more sophisticated functions always halt. For example, the Ackermann function
, which is not primitive recursive, nevertheless is a total computable function computable by a term rewriting system with a reduction ordering
on its arguments (Ohlebusch, 2002, pp.67).
The answer to each of these questions is no.
The following theorem shows that the functions computable by machines that always halt do not include extensions of all partial computable functions, which implies the first question above has a negative answer. This fact is closely related to the algorithmic unsolvability of the Halting problem
.
The proof proceeds by contradiction. If g were a total computable function extending f then g would be computable by some Turing machine; fix e as the index of such a machine. Build a Turing machine M, using Kleene's recursion theorem
, which on input 0 simulates the machine with index e running on an index nM for M (thus the machine M can produce an index of itself; this is the role of the recursion theorem). By assumption, this simulation will eventually return an answer. Define M so that if g(nM) = m then the return value of M is m + 1. Thus f(nM), the true return value of M on input 0, will not equal g(nM). This contradicts the assumption that g extends f.
The second question asks, in essence, whether there is another reasonable model of computation which computes only total functions and computes all the total computable functions. Informally, if such a model existed then each of its computers could be simulated by a Turing machine. Thus if this new model of computation consisted of a sequence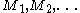
of machines, there would be a recursively enumerable sequence 
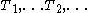of Turing machines that compute total functions and so that every total computable function is computable by one of the machines Ti. This is impossible, because a machine 
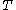could be constructed such that on input i the machine T returns 
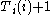. This machine cannot be equivalent to any machine T on the list: suppose it were on the list at index j. Then 
, which does not return an integer result. Therefore it can't be total, but the function by construction must be total (if total functions are recursively enumerable, then this function can be constructed), so we have a contradiction. This shows that the second question has a negative answer.
of whether the Turing machine with index e will halt on every input is not decidable. In fact, this problem is at level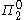
of the arithmetical hierarchy
. Thus this problem is strictly more difficult than the Halting problem
, which asks whether the machine with index e halts on input 0. Intuitively, this difference in unsolvability is because each instance of the "total machine" problem represents infinitely many instances of the Halting problem.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, a machine that always halts—also called a decider (Sipser, 1996) or a total Turing machine (Kozen, 1997)—is a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
that halts for every input.
Because it always halts, the machine is able to decide whether a given string is a member of a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. The class of languages which can be decided by such machines is exactly the set of recursive language
Recursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
s. However, due to the Halting Problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
, determining whether an arbitrary Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
halts on an arbitrary input is itself an undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
.
Functions computable by total Turing machines
In practice, many functions of interest are computable by machines that always halt. A machine that uses only finite memory on any particular input can be forced to halt for every input by restricting its flow controlControl flow
In computer science, control flow refers to the order in which the individual statements, instructions, or function calls of an imperative or a declarative program are executed or evaluated....
capabilities so that no input will ever cause the machine to enter an infinite loop
Infinite loop
An infinite loop is a sequence of instructions in a computer program which loops endlessly, either due to the loop having no terminating condition, having one that can never be met, or one that causes the loop to start over...
. As a trivial example, a machine implementing a finitary decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
will always halt.
It is not required that the machine be entirely free of looping capabilities, however, to guarantee halting. If we restrict loops to be of a predictably finite size (not unlike the FOR loop in BASIC
BASIC
BASIC is a family of general-purpose, high-level programming languages whose design philosophy emphasizes ease of use - the name is an acronym from Beginner's All-purpose Symbolic Instruction Code....
), we can express all of the primitive recursive functions (Meyer and Ritchie, 1967). An example of such a machine is provided by the toy programming language PL-{GOTO} of Brainerd and Landweber (1974).
We can further define a programming language in which we can ensure that even more sophisticated functions always halt. For example, the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
, which is not primitive recursive, nevertheless is a total computable function computable by a term rewriting system with a reduction ordering
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
on its arguments (Ohlebusch, 2002, pp.67).
Relationship to partial Turing machines
A general Turing machine will compute a partial function. Two questions can be asked about the relationship between partial Turing machines and total Turing machines:- Can every partial function computable by a partial Turing machine be extended (that is, have its domain enlarged) to become a total computable function?
- Is it possible to change the definition of a Turing machine so that a particular class of total Turing machines, computing all the total computable functions, can be found?
The answer to each of these questions is no.
The following theorem shows that the functions computable by machines that always halt do not include extensions of all partial computable functions, which implies the first question above has a negative answer. This fact is closely related to the algorithmic unsolvability of the Halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
.
- Theorem. There are Turing computable partial functions that have no extension to a total Turing computable function. In particular, the partial function f defined so that f(n) = m if and only if the Turing machine with index n halts on input 0 with output m has no extension to a total computable function.
The proof proceeds by contradiction. If g were a total computable function extending f then g would be computable by some Turing machine; fix e as the index of such a machine. Build a Turing machine M, using Kleene's recursion theorem
Kleene's recursion theorem
In computability theory, Kleene's recursion theorems are a pair of fundamental results about the application of computable functions to their own descriptions...
, which on input 0 simulates the machine with index e running on an index nM for M (thus the machine M can produce an index of itself; this is the role of the recursion theorem). By assumption, this simulation will eventually return an answer. Define M so that if g(nM) = m then the return value of M is m + 1. Thus f(nM), the true return value of M on input 0, will not equal g(nM). This contradicts the assumption that g extends f.
The second question asks, in essence, whether there is another reasonable model of computation which computes only total functions and computes all the total computable functions. Informally, if such a model existed then each of its computers could be simulated by a Turing machine. Thus if this new model of computation consisted of a sequence
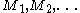of machines, there would be a recursively enumerable sequence 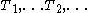of Turing machines that compute total functions and so that every total computable function is computable by one of the machines Ti. This is impossible, because a machine 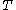could be constructed such that on input i the machine T returns 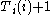. This machine cannot be equivalent to any machine T on the list: suppose it were on the list at index j. Then , which does not return an integer result. Therefore it can't be total, but the function by construction must be total (if total functions are recursively enumerable, then this function can be constructed), so we have a contradiction. This shows that the second question has a negative answer.The set of indices of total Turing machines
The decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
of whether the Turing machine with index e will halt on every input is not decidable. In fact, this problem is at level
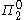of the arithmetical hierarchyArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
. Thus this problem is strictly more difficult than the Halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
, which asks whether the machine with index e halts on input 0. Intuitively, this difference in unsolvability is because each instance of the "total machine" problem represents infinitely many instances of the Halting problem.