
MU puzzle
Encyclopedia
The MU puzzle is a puzzle stated by Douglas Hofstadter
and found in Gödel, Escher, Bach
. As stated, it is an example of a Post canonical system
and can be reformulated as a string rewriting system.
Using these four rules is it possible to change
The production rules can be written in a more schematic way. Suppose
can be written as:
Is it possible to obtain the word
In order to prove assertions like this, it is often beneficial to look for an invariant
, that is some quantity or property that doesn't change while applying the rules.
In this case, one can look at the total number of
Thus, the goal of
In the language of modular arithmetic
, the number of
of 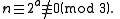
where counts how often the second rule is applied.
counts how often the second rule is applied.
in mathematical logic. The MIU system can be viewed as a formal logic in which a string is considered provable if it can be derived by application of the rules starting from MI. In this interpretation, the question is phrased as "Is MU provable in the MIU logic?".
Finding an invariant of the inference rules is a common method for establishing independence results.
Douglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
and found in Gödel, Escher, Bach
Gödel, Escher, Bach
Gödel, Escher, Bach: An Eternal Golden Braid is a book by Douglas Hofstadter, described by his publishing company as "a metaphorical fugue on minds and machines in the spirit of Lewis Carroll"....
. As stated, it is an example of a Post canonical system
Post canonical system
A Post canonical system, as created by Emil Post, is a string-manipulation system that starts with finitely-many strings and repeatedly transforms them by applying a finite set of specified rules of a certain form, thus generating a formal language...
and can be reformulated as a string rewriting system.
The puzzle
Suppose there are the symbolsM, I, and U which can be combined to produce strings of symbols called "words". The MU puzzle asks one to start with the "axiomatic" word MI and transform it into the word MU using in each step one of the following transformation rules:
- Add a
Uto the end of any string ending inI. For example:MItoMIU. - Double any string after the
M(that is, changeMx, toMxx). For example:MIUtoMIUIU. - Replace any
IIIwith aU. For example:MUIIIUtoMUUU. - Remove any
UU. For example:MUUUtoMU.
Using these four rules is it possible to change
MI into MU in a finite number of steps?The production rules can be written in a more schematic way. Suppose
x and y behave as variables (standing for strings of symbols). Then the production rulesFormal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
can be written as:
-
xI → xIU -
Mx → Mxx -
xIIIy → xUy -
xUUy → xy
Is it possible to obtain the word
MU using these rules?Solution
The puzzle's solution is no. It is impossible to change the stringMI into MU by repeatedly applying the given rules.In order to prove assertions like this, it is often beneficial to look for an invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
, that is some quantity or property that doesn't change while applying the rules.
In this case, one can look at the total number of
I in a string. Only the second and third rules change this number. In particular, rule two will double it while rule three will reduce it by 3. Now, the invariant property is that the number of I is not divisible by 3:
- In the beginning, the number of
Is is 1 which is not divisible by 3. - Doubling a number that is not divisible by 3 does not make it divisible by 3.
- Subtracting 3 from a number that is not divisible by 3 does not make it divisible by 3 either.
Thus, the goal of
MU with zero I cannot be achieved because 0 is divisible by 3.In the language of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, the number
 of
of I obeys the congruence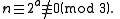
where
 counts how often the second rule is applied.
counts how often the second rule is applied.Relationship to provability
The result that MU cannot be obtained with these rules demonstrates the notion of independenceIndependence (mathematical logic)
In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
in mathematical logic. The MIU system can be viewed as a formal logic in which a string is considered provable if it can be derived by application of the rules starting from MI. In this interpretation, the question is phrased as "Is MU provable in the MIU logic?".
Finding an invariant of the inference rules is a common method for establishing independence results.

