
M. Riesz extension theorem
Encyclopedia
The M. Riesz extension theorem is a theorem
in mathematics
, proved by Marcel Riesz
during his study of the problem of moments.
vector space
, F ⊂ E a vector subspace, and let K ⊂ E be a convex cone
.
A linear functional
φ: F → R is called K-positive, if
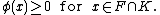
A linear functional ψ: E → R is called a K-positive extension of φ if
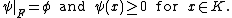
In general, a K-positive linear functional on F can not be extended to a -positive linear functional on E. Already in two dimensions one obtains a counterexample taking K to be the upper halfplane with the open negative x-axis removed. If F is the real axis, then the positive functional φ(x, 0) = x can not be extended to a positive functional on the plane.
-positive linear functional on E. Already in two dimensions one obtains a counterexample taking K to be the upper halfplane with the open negative x-axis removed. If F is the real axis, then the positive functional φ(x, 0) = x can not be extended to a positive functional on the plane.
However, the extension exists under the additional assumption that for every y ∈ E there exists x∈F such that y − x ∈K; in other words, if E = K + F.
it is sufficient to consider the case dim E/F = 1.
Choose y ∈ E\F. Set
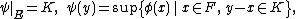
and extend ψ to E by linearity. Let us show that ψ is K-positive.
Every point z in K is a positive linear multiple of either x + y or x − y for some x ∈ F. In the first case, z = a(y + x), therefore y = z/a − x. Hence

therefore ψ(z) ≥ 0. In the second case, z = a(x − y), therefore y = x − z/a. Let x1 ∈ F be such that z1 = y − x1 ∈ K and ψ(x1) ≥ ψ(y) − ε. Then

therefore ψ(z) ≥ −a ε. Since this is true for arbitrary ε > 0, we obtain ψ(z) ≥ 0.
linear space, and let K ⊂ E be a convex cone
. Let x ∈ E\(−K) be such that R x + K = E. Then there exists a K-positive linear functional φ: E → R such that φ(x) > 0.
Let V be a linear space, and let N be a sublinear function on V. Let φ be a functional on a subspace U ⊂ V that is dominated by N:
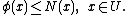
The Hahn–Banach theorem asserts that φ can be extended to a linear functional on V that is dominated by N.
To derive this from the M. Riesz extension theorem, define a convex cone K ⊂ R×V by

Define a functional φ1 on R×U by
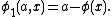
One can see that φ1 is K-positive, and that K + (R × U) = V. Therefore φ1 can be extended to a K-positive functional ψ1 on R×V. Then
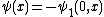
is the desired extension of φ. Indeed, if ψ(x) > N(x), we have: (N(x), x) ∈ K, whereas
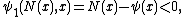
leading to a contradiction.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, proved by Marcel Riesz
Marcel Riesz
Marcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
during his study of the problem of moments.
Formulation
Let E be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, F ⊂ E a vector subspace, and let K ⊂ E be a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
.
A linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
φ: F → R is called K-positive, if
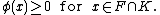
A linear functional ψ: E → R is called a K-positive extension of φ if
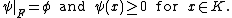
In general, a K-positive linear functional on F can not be extended to a
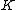 -positive linear functional on E. Already in two dimensions one obtains a counterexample taking K to be the upper halfplane with the open negative x-axis removed. If F is the real axis, then the positive functional φ(x, 0) = x can not be extended to a positive functional on the plane.
-positive linear functional on E. Already in two dimensions one obtains a counterexample taking K to be the upper halfplane with the open negative x-axis removed. If F is the real axis, then the positive functional φ(x, 0) = x can not be extended to a positive functional on the plane.However, the extension exists under the additional assumption that for every y ∈ E there exists x∈F such that y − x ∈K; in other words, if E = K + F.
Proof
By transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
it is sufficient to consider the case dim E/F = 1.
Choose y ∈ E\F. Set
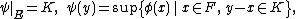
and extend ψ to E by linearity. Let us show that ψ is K-positive.
Every point z in K is a positive linear multiple of either x + y or x − y for some x ∈ F. In the first case, z = a(y + x), therefore y = z/a − x. Hence

therefore ψ(z) ≥ 0. In the second case, z = a(x − y), therefore y = x − z/a. Let x1 ∈ F be such that z1 = y − x1 ∈ K and ψ(x1) ≥ ψ(y) − ε. Then

therefore ψ(z) ≥ −a ε. Since this is true for arbitrary ε > 0, we obtain ψ(z) ≥ 0.
Corollary: Krein's extension theorem
Let E be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
linear space, and let K ⊂ E be a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
. Let x ∈ E\(−K) be such that R x + K = E. Then there exists a K-positive linear functional φ: E → R such that φ(x) > 0.
Connection to the Hahn–Banach theorem
The Hahn–Banach theorem can be deduced from the M. Riesz extension theorem.Let V be a linear space, and let N be a sublinear function on V. Let φ be a functional on a subspace U ⊂ V that is dominated by N:
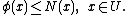
The Hahn–Banach theorem asserts that φ can be extended to a linear functional on V that is dominated by N.
To derive this from the M. Riesz extension theorem, define a convex cone K ⊂ R×V by

Define a functional φ1 on R×U by
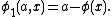
One can see that φ1 is K-positive, and that K + (R × U) = V. Therefore φ1 can be extended to a K-positive functional ψ1 on R×V. Then
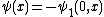
is the desired extension of φ. Indeed, if ψ(x) > N(x), we have: (N(x), x) ∈ K, whereas
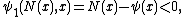
leading to a contradiction.

