Lyapunov equation
Encyclopedia
In control theory
, the discrete Lyapunov equation is of the form
where
is a Hermitian matrix and 
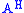is the conjugate transpose
of
. The continuous Lyapunov equation is of form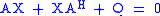
.
The Lyapunov equation occurs in many branches of control theory, such as stability analysis
and optimal control
. This and related equations are named after the Russian mathematician Aleksandr Lyapunov
.
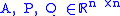, and 
and 
are symmetric. The notation 
means that the matrix 
is positive definite
Theorem (continuous time version). If there exist
and 
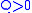satisfying 
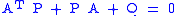then the linear system 
is globally asymptotically stable. The quadratic function 
is a Lyapunov function
that can be used to verify stability.
Theorem (discrete time version). If there exist
and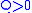 
satisfying 
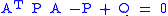then the linear system 
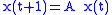is globally asymptotically stable. As before, 
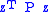is a Lyapunov function.
s, be written as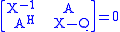
or equivalently as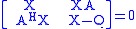
.
Specialized software is available for solving Lyapunov equations. For the discrete case, the Schur method of Kitagawa (1977) is often used. For the continuous Lyapunov equation the method of Bartels and Stewart (1972) can be used.
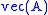operator as stacking the columns of a matrix 
. Further define 
as the kronecker product of 
and 
. Using the result that
,
one has
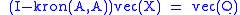
where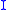
is a conformable identity matrix One may then solve for 
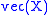by inverting or solving the linear equations. To get 
, one must just reshape 
appropriately.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, the discrete Lyapunov equation is of the form
where
is a Hermitian matrix and 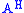is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of
. The continuous Lyapunov equation is of form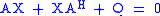.The Lyapunov equation occurs in many branches of control theory, such as stability analysis
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
and optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
. This and related equations are named after the Russian mathematician Aleksandr Lyapunov
Aleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
.
Application to stability
In the following theorems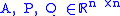, and and are symmetric. The notation means that the matrix is positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
Theorem (continuous time version). If there exist
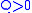and satisfying 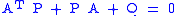then the linear system is globally asymptotically stable. The quadratic function is a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
that can be used to verify stability.
Theorem (discrete time version). If there exist
and 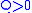satisfying 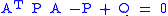then the linear system 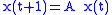is globally asymptotically stable. As before, 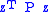is a Lyapunov function.Computational aspects of solution
The discrete Lyapunov equations can, by using Schur complementSchur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
s, be written as
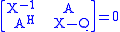
or equivalently as
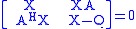.Specialized software is available for solving Lyapunov equations. For the discrete case, the Schur method of Kitagawa (1977) is often used. For the continuous Lyapunov equation the method of Bartels and Stewart (1972) can be used.
Analytic Solution
There is an analytic solution to the discrete time equations. Define the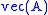 operator as stacking the columns of a matrix . Further define as the kronecker product of and . Using the result that,one has
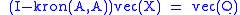
where
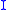is a conformable identity matrix One may then solve for 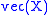by inverting or solving the linear equations. To get , one must just reshape appropriately.