Lumpability
Encyclopedia
In probability theory
, lumpability is a method for reducing the size of the state space of some continuous-time Markov chains, first published by Kemeny
and Snell.
is divided into disjoint subsets of states, where these subsets are denoted by ti. This forms a partition
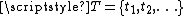of the states. Both the state-space and the collection of subsets may be either finite or countably infinite.
A continuous-time Markov chain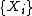
is lumpable with respect to the partition T if and only if, for any subsets ti and tj in the partition, and for any states n,n’ in subset ti,
where q(i,j) is the transition rate from state i to state j.
Similarly, for a stochastic matrix
P, P is a lumpable matrix on a partition T if and only if and only if, for any subsets ti and tj in the partition, and for any states n,n’ in subset ti,
where p(i,j) is the probability of moving from state i to state j.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, lumpability is a method for reducing the size of the state space of some continuous-time Markov chains, first published by Kemeny
John George Kemeny
John George Kemeny was a Hungarian American mathematician, computer scientist, and educator best known for co-developing the BASIC programming language in 1964 with Thomas E. Kurtz. Kemeny served as the 13th President of Dartmouth College from 1970 to 1981 and pioneered the use of computers in...
and Snell.
Definition
Suppose that the complete state-space of a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
is divided into disjoint subsets of states, where these subsets are denoted by ti. This forms a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
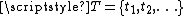of the states. Both the state-space and the collection of subsets may be either finite or countably infinite.A continuous-time Markov chain
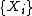is lumpable with respect to the partition T if and only if, for any subsets ti and tj in the partition, and for any states n,n’ in subset ti,
where q(i,j) is the transition rate from state i to state j.
Similarly, for a stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
P, P is a lumpable matrix on a partition T if and only if and only if, for any subsets ti and tj in the partition, and for any states n,n’ in subset ti,
where p(i,j) is the probability of moving from state i to state j.
Example
Consider the matrix-
and notice it is lumpable on the partition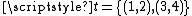
so we write
-
and call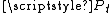
the lumped matrix of P on t.
Quasi–lumpability
Franceschinis and Muntz introduced quasi-lumpability, a property whereby a small change in the rate matrix makes the chain lumpable.
-