Lucky number
Encyclopedia
In number theory
, a lucky number is a natural number
in a set which is generated by a "sieve
" similar to the Sieve of Eratosthenes
that generates the prime
s.
Begin with a list of integer
s starting with 1:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
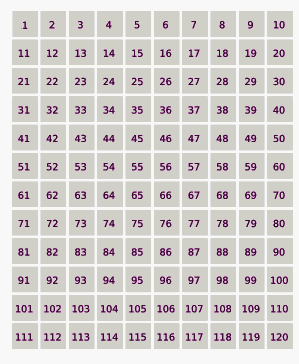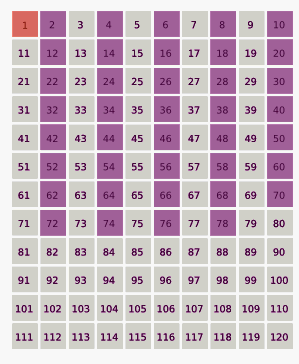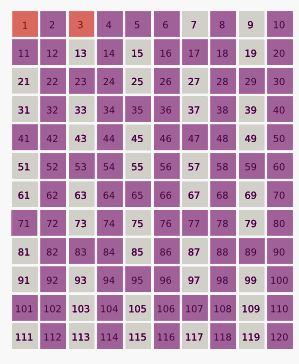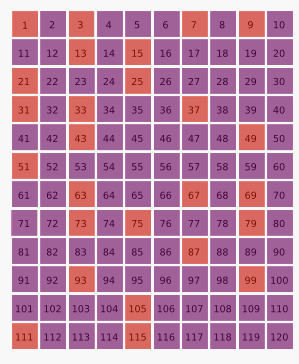
Every second number (all even numbers) is eliminated, leaving only the odd integers:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25,
The second term in this sequence
is 3. Every third number which remains in the list is eliminated:
1, 3, 7, 9, 13, 15, 19, 21, 25,
The third surviving number is now 7, so every seventh number that remains is eliminated:
1, 3, 7, 9, 13, 15, 21, 25,
As this procedure is repeated indefinitely, the survivors are the lucky numbers:
 The term was introduced in 1955 in a paper by Gardiner, Lazarus, Metropolis
The term was introduced in 1955 in a paper by Gardiner, Lazarus, Metropolis
and Ulam. They suggest also calling its defining sieve the sieve of Josephus
Flavius because of its similarity with the counting-out game in the Josephus problem
.
Lucky numbers share some properties with primes, such as asymptotic behaviour according to the prime number theorem
; also, a version of Goldbach's conjecture
has been extended to them. There are infinitely many lucky numbers. Because of these apparent connections with the prime numbers, some mathematicians have suggested that these properties may be found in a larger class of sets of numbers generated by sieves of a certain unknown form, although there is little theoretical basis for this conjecture
. Twin lucky numbers and twin prime
s also appear to occur with similar frequency.
A lucky prime is a lucky number that is prime. It is not known whether there are infinitely many lucky primes. The first few are
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a lucky number is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
in a set which is generated by a "sieve
Sieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
" similar to the Sieve of Eratosthenes
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
that generates the prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s.
Begin with a list of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s starting with 1:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
Every second number (all even numbers) is eliminated, leaving only the odd integers:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25,
The second term in this sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
is 3. Every third number which remains in the list is eliminated:
1, 3, 7, 9, 13, 15, 19, 21, 25,
The third surviving number is now 7, so every seventh number that remains is eliminated:
1, 3, 7, 9, 13, 15, 21, 25,
As this procedure is repeated indefinitely, the survivors are the lucky numbers:
- 1, 3, 7, 9, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 1515 (number)15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 2121 (number)21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 2525 (number)25 is the natural number following 24 and preceding 26.-In mathematics:It is a square number, being 5² = 5 × 5. It is the smallest square that is also a sum of two squares: 25 = 3² + 4²...
, 3131 (number)31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,...
, 3333 (number)33 is the natural number following 32 and preceding 34.-In mathematics:33 is the largest positive integer that cannot be expressed as a sum of different triangular numbers. It is also the smallest odd repdigit that is not a prime number.33 is the eighth distinct semiprime comprising the prime...
, 3737 (number)37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
, 4343 (number)43 is the natural number following 42 and preceding 44.- In mathematics :Forty-three is the 14th smallest prime number. The previous is forty-one, with which it comprises a twin prime, and the next is forty-seven. 43 is the smallest prime that is not a Chen prime...
, 4949 (number)49 is the natural number following 48 and preceding 50.-In mathematics:* Forty-nine is the square of seven and is therefore the fourth squared prime number.The aliquot sum of forty-nine is 8...
, 51, 6363 (number)63 is a natural number following 62 and preceding 64.-In mathematics:Although a number of the form 2n - 1, 63 is not a Mersenne prime since n is not prime and 63 is certainly not prime either. It is a Woodall number and a Harshad number. It is a highly cototient number. It is a repdigit in base 4...
, 6767 (number)67 is the natural number following 66 and preceding 68. It is an odd number.-In mathematics:Sixty-seven is the 19th prime number , an irregular prime, a lucky prime, the sum of five consecutive primes , and a Heegner number.Since 18! + 1 is divisible by 67 but 67 is not one more than a multiple of...
, 6969 (number)69 is a number following 68 and preceding 70.- In mathematics:The aliquot sum of sixty-nine is 27 within the aliquot sequence 69 being the third composite number in the 13-aliquot tree.69 is a semiprime...
, 7373 (number)73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :...
, 7575 (number)75 is the natural number following 74 and preceding 76.-In mathematics:As the sum of the first five pentagonal numbers, seventy-five is a pentagonal pyramidal number. It is also an enneagonal number....
, 7979 (number)Seventy-nine is the natural number following 78 and preceding 80.79 may represent:-In mathematics:*An odd number*The smallest number that can't be represented as a sum of fewer than 19 fourth powers*A strictly non-palindromic number...
, 8787 (number)87 is the natural number following 86 and preceding 88.-In mathematics:Eighty-seven is the twenty-sixth distinct semiprime and the eighth of the form . The aliquot sum of 87 is 33 within the aliquot sequence 86 being the eighteenth composite number in the 3-aliquot tree.Eighty-seven is the sum of...
, 9393 (number)93 is the natural number following 92 and preceding 94.-In mathematics:Ninety-three is the twenty-eighth distinct semiprime and the ninth of the form...
, 9999 (number)99 is the natural number following 98 and preceding 100.-Mathematics:99 is the ninth repdigit, a palindromic number and a Kaprekar number...
, ... .

Nicholas Metropolis
Nicholas Constantine Metropolis was a Greek American physicist.-Work:Metropolis received his B.Sc. and Ph.D. degrees in physics at the University of Chicago...
and Ulam. They suggest also calling its defining sieve the sieve of Josephus
Josephus
Titus Flavius Josephus , also called Joseph ben Matityahu , was a 1st-century Romano-Jewish historian and hagiographer of priestly and royal ancestry who recorded Jewish history, with special emphasis on the 1st century AD and the First Jewish–Roman War, which resulted in the Destruction of...
Flavius because of its similarity with the counting-out game in the Josephus problem
Josephus problem
In computer science and mathematics, the Josephus Problem is a theoretical problem related to a certain counting-out game....
.
Lucky numbers share some properties with primes, such as asymptotic behaviour according to the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
; also, a version of Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
has been extended to them. There are infinitely many lucky numbers. Because of these apparent connections with the prime numbers, some mathematicians have suggested that these properties may be found in a larger class of sets of numbers generated by sieves of a certain unknown form, although there is little theoretical basis for this conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
. Twin lucky numbers and twin prime
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
s also appear to occur with similar frequency.
A lucky prime is a lucky number that is prime. It is not known whether there are infinitely many lucky primes. The first few are
- 3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193 .
External links
- Peterson, Ivars. MathTrek: Martin Gardner's Lucky Number
- Lucky Numbers by Enrique Zeleny, The Wolfram Demonstrations Project.

