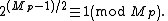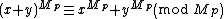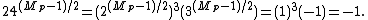Lucas–Lehmer test for Mersenne numbers
Encyclopedia
In mathematics
, the Lucas–Lehmer test (LLT) is a primality test
for Mersenne number
s. The test was originally developed by Édouard Lucas
in 1856, and subsequently improved by Lucas in 1878 and Derrick Henry Lehmer
in the 1930s.
for establishing its primality). Define a sequence {s i } for all i ≥ 0 by
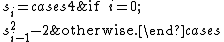
The first few terms of this sequence are 4, 14, 194, 37634, ... .
Then Mp is prime iff
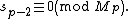
The number sp − 2 mod Mp is called the Lucas–Lehmer residue of p. (Some authors equivalently set s1 = 4 and test sp−1 mod Mp). In pseudocode, the test might be written:
// Determine if Mp = 2p − 1 is prime
Lucas–Lehmer(p)
var s = 4
var M = 2p − 1
repeat p − 2 times:
s = ((s × s) − 2) mod M
if s = 0 return PRIME else return COMPOSITE
By performing the
.
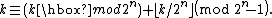
In other words, if we take the least significant n bits of k, and add the remaining bits of k, and then do this repeatedly until at most n bits remain, we can compute the remainder after dividing k by the Mersenne number 2n−1 without using division. For example:
Moreover, since
With the modulus out of the way, the asymptotic complexity of the algorithm depends only on the multiplication algorithm
used to square s at each step. The simple "grade-school" algorithm for multiplication requires O
(p2) bit-level or word-level operations to square a p-bit number, and since we do this O(p) times, the total time complexity is O(p3). A more efficient multiplication method, the Schönhage–Strassen algorithm based on the Fast Fourier transform
, requires O(p log p log log p) time to square a p-bit number, reducing the complexity to O(p2 log p log log p) or Õ(p2).. Currently the most efficient known multiplication algorithm, Fürer's algorithm
, needs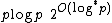 time to multiply two p-bit numbers.
time to multiply two p-bit numbers.
By comparison, the most efficient randomized primality test for general integers, the Miller–Rabin primality test, takes O(k p2 log p log log p) bit operations using FFT multiplication for a p-digit number (here p can be any natural number, not necessarily a prime), where k is the number of iterations and is related to the error rate. So it is in the same complexity class as the Lucas-Lehmer test for constant k. But in practice the cost of doing many iterations and other differences leads to worse performance for Miller–Rabin. The most efficient deterministic primality test for general integers, the AKS primality test
, requires Õ(p6) bit operations in its best known variant and is dramatically slower in practice.
Because we end with s set to zero, M3 is prime.
On the other hand, M11 = 2047 = 23 × 89 is not prime. To show this, we start with s set to 4 and update it 11−2 = 9 times, taking the results mod 2047:
Because s is not zero, M11=2047 is not prime. Notice that we learn nothing about the factors of 2047, only its Lucas–Lehmer residue, 1736.
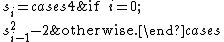
Then our theorem is that Mp is prime iff
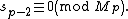
We begin by noting that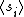 is a recurrence relation
is a recurrence relation
with a closed-form solution. Define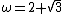 and
and 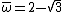 ; then we can verify by induction
; then we can verify by induction
that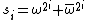 for all i:
for all i:
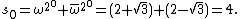
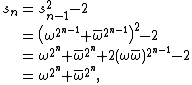
where the last step follows from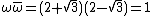 . We will use this in both parts.
. We will use this in both parts.
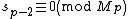 implies that
implies that 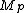 is prime. We relate a straightforward proof exploiting elementary group theory
is prime. We relate a straightforward proof exploiting elementary group theory
given by J. W. Bruce as related by Jason Wojciechowski.
Suppose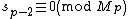 . Then
. Then 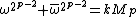 for some integer k, and:
for some integer k, and: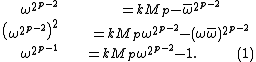
Now suppose Mp is composite, and let q be the smallest prime factor of Mp. Since Mersenne numbers are odd, we have q > 2. Define the set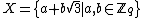 with q2 elements, where
with q2 elements, where 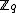 is the integers mod q, a finite field
is the integers mod q, a finite field
(in the language of ring theory
X is the quotient of the univariate polynomial ring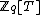 by the ideal generated by
by the ideal generated by 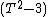 ). The multiplication operation in
). The multiplication operation in 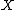 is defined by:
is defined by:
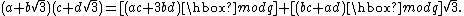
Since q > 2, and
and 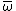 are in
are in 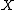 (in fact
(in fact 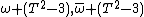 are in X, but by abuse of language we identify
are in X, but by abuse of language we identify 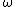 and
and 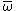 with their images in X under the natural ring homomorphism from
with their images in X under the natural ring homomorphism from 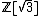 to X which sends the square root of 3 to T). Any product of two numbers in X is in X, but it's not a group
to X which sends the square root of 3 to T). Any product of two numbers in X is in X, but it's not a group
under multiplication because not every element x has an inverse y such that xy = 1 (in fact X is a ring
and the set of non-zero elements of X is a group if and only if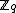 does not contain a square root of 3). If we consider only the elements that have inverses, we get a group X* of size at most
does not contain a square root of 3). If we consider only the elements that have inverses, we get a group X* of size at most 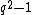 (since 0 has no inverse).
(since 0 has no inverse).
Now, since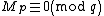 , and
, and 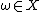 , we have
, we have 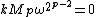 in X, which by equation (1) gives
in X, which by equation (1) gives 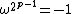 . Squaring both sides gives
. Squaring both sides gives 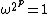 , showing that
, showing that 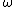 is invertible with inverse
is invertible with inverse 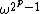 and so lies in X*, and moreover has an order
and so lies in X*, and moreover has an order
dividing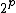 . In fact the order must equal
. In fact the order must equal 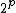 , since
, since 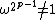 and so the order does not divide
and so the order does not divide 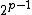 . Since the order of an element is at most the order (size) of the group, we conclude that
. Since the order of an element is at most the order (size) of the group, we conclude that 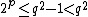 . But since q is the smallest prime factor of the composite
. But since q is the smallest prime factor of the composite 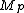 , we must have
, we must have 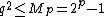 , yielding the contradiction
, yielding the contradiction 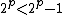 . So
. So 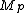 is prime.
is prime.
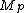 is prime and show
is prime and show 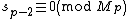 . We rely on a simplification of a proof by Öystein J. R.
. We rely on a simplification of a proof by Öystein J. R.
Ödseth. First, notice that 3 is a quadratic non-residue mod Mp, since 2 p − 1 for odd p > 1 only takes on the value 7 mod 12, and so the Legendre symbol
properties tell us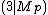 is −1. Euler's criterion
is −1. Euler's criterion
then gives us:
On the other hand, 2 is a quadratic residue mod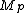 , since
, since 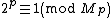 and so
and so 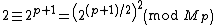 . Euler's criterion again gives:
. Euler's criterion again gives:
Next, define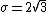 , and define X* similarly as before as the multiplicative group of
, and define X* similarly as before as the multiplicative group of 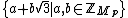 . We will use the following lemmas:
. We will use the following lemmas:
(from Proofs of Fermat's little theorem#Proof using the binomial theorem)
for every integer a (Fermat's little theorem
)
Then, in the group X* we have:
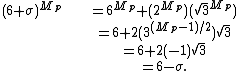
We chose such that
such that 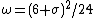 . Consequently, we can use this to compute
. Consequently, we can use this to compute 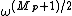 in the group X*:
in the group X*:
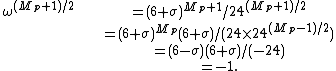
where we use the fact that
Since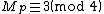 , all that remains is to multiply both sides of this equation by
, all that remains is to multiply both sides of this equation by 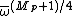 and use
and use 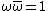 :
:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lucas–Lehmer test (LLT) is a primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
for Mersenne number
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
s. The test was originally developed by Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
in 1856, and subsequently improved by Lucas in 1878 and Derrick Henry Lehmer
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
in the 1930s.
The test
The Lucas–Lehmer test works as follows. Let Mp = 2p − 1 be the Mersenne number to test with p an odd prime (because p is exponentially smaller than Mp, we can use a simple algorithm like trial divisionTrial division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. Its ease of implementation makes it a viable integer factorization option for devices with little available memory, such as graphing calculators....
for establishing its primality). Define a sequence {s i } for all i ≥ 0 by
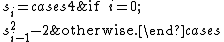
The first few terms of this sequence are 4, 14, 194, 37634, ... .
Then Mp is prime iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
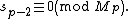
The number sp − 2 mod Mp is called the Lucas–Lehmer residue of p. (Some authors equivalently set s1 = 4 and test sp−1 mod Mp). In pseudocode, the test might be written:
// Determine if Mp = 2p − 1 is prime
Lucas–Lehmer(p)
var s = 4
var M = 2p − 1
repeat p − 2 times:
s = ((s × s) − 2) mod M
if s = 0 return PRIME else return COMPOSITE
By performing the
mod M at each iteration, we ensure that all intermediate results are at most p bits (otherwise the number of bits would double each iteration). It is exactly the same strategy employed in modular exponentiationModular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
.
Time complexity
In the algorithm as written above, there are two expensive operations during each iteration: the multiplications × s, and the mod M operation. The mod M operation can be made particularly efficient on standard binary computers by observing the following simple property: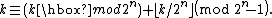
In other words, if we take the least significant n bits of k, and add the remaining bits of k, and then do this repeatedly until at most n bits remain, we can compute the remainder after dividing k by the Mersenne number 2n−1 without using division. For example:
| 916 mod 25−1 | = | 11100101002 mod 25−1 |
| = | 111002 + 101002 mod 25−1 | |
| = | 1100002 mod 25−1 | |
| = | 12 + 100002 mod 25−1 | |
| = | 100012 mod 25−1 | |
| = | 100012 | |
| = | 17. |
Moreover, since
s × s will never exceed M2 < 22p, this simple technique converges in at most 2 p-bit additions, which can be done in linear time. As a small exceptional case, the above algorithm may produce 2n−1 for a multiple of the modulus, rather than the correct value of zero; this should be accounted for.With the modulus out of the way, the asymptotic complexity of the algorithm depends only on the multiplication algorithm
Multiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
used to square s at each step. The simple "grade-school" algorithm for multiplication requires O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(p2) bit-level or word-level operations to square a p-bit number, and since we do this O(p) times, the total time complexity is O(p3). A more efficient multiplication method, the Schönhage–Strassen algorithm based on the Fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, requires O(p log p log log p) time to square a p-bit number, reducing the complexity to O(p2 log p log log p) or Õ(p2).. Currently the most efficient known multiplication algorithm, Fürer's algorithm
Fürer's algorithm
Fürer's algorithm is an integer multiplication algorithm for very large numbers possessing a very low asymptotic complexity. It was created in 2007 by Swiss mathematician Martin Fürer of Pennsylvania State University as an asymptotically faster algorithm than its predecessor, the...
, needs
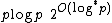 time to multiply two p-bit numbers.
time to multiply two p-bit numbers.By comparison, the most efficient randomized primality test for general integers, the Miller–Rabin primality test, takes O(k p2 log p log log p) bit operations using FFT multiplication for a p-digit number (here p can be any natural number, not necessarily a prime), where k is the number of iterations and is related to the error rate. So it is in the same complexity class as the Lucas-Lehmer test for constant k. But in practice the cost of doing many iterations and other differences leads to worse performance for Miller–Rabin. The most efficient deterministic primality test for general integers, the AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
, requires Õ(p6) bit operations in its best known variant and is dramatically slower in practice.
Examples
Suppose we wish to verify that M3 = 7 is prime using the Lucas–Lehmer test. We start out with s set to 4 and then update it 3−2 = 1 time, taking the results mod 7:- s ← ((4 × 4) − 2) mod 7 = 0
Because we end with s set to zero, M3 is prime.
On the other hand, M11 = 2047 = 23 × 89 is not prime. To show this, we start with s set to 4 and update it 11−2 = 9 times, taking the results mod 2047:
- s ← ((4 × 4) − 2) mod 2047 = 14
- s ← ((14 × 14) − 2) mod 2047 = 194
- s ← ((194 × 194) − 2) mod 2047 = 788
- s ← ((788 × 788) − 2) mod 2047 = 701
- s ← ((701 × 701) − 2) mod 2047 = 119
- s ← ((119 × 119) − 2) mod 2047 = 1877
- s ← ((1877 × 1877) − 2) mod 2047 = 240
- s ← ((240 × 240) − 2) mod 2047 = 282
- s ← ((282 × 282) − 2) mod 2047 = 1736
Because s is not zero, M11=2047 is not prime. Notice that we learn nothing about the factors of 2047, only its Lucas–Lehmer residue, 1736.
Proof of correctness
Lehmer's original proof of the correctness of this test is complex, so we'll depend upon more recent refinements. Recall the definition: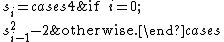
Then our theorem is that Mp is prime iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
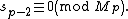
We begin by noting that
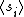 is a recurrence relation
is a recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
with a closed-form solution. Define
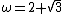 and
and 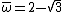 ; then we can verify by induction
; then we can verify by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that
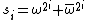 for all i:
for all i: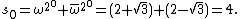
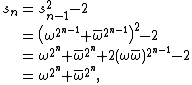
where the last step follows from
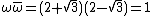 . We will use this in both parts.
. We will use this in both parts.Sufficiency
In this direction we wish to show that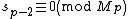 implies that
implies that 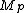 is prime. We relate a straightforward proof exploiting elementary group theory
is prime. We relate a straightforward proof exploiting elementary group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
given by J. W. Bruce as related by Jason Wojciechowski.
Suppose
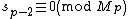 . Then
. Then 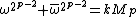 for some integer k, and:
for some integer k, and: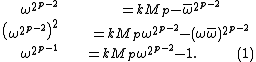
Now suppose Mp is composite, and let q be the smallest prime factor of Mp. Since Mersenne numbers are odd, we have q > 2. Define the set
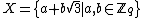 with q2 elements, where
with q2 elements, where 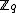 is the integers mod q, a finite field
is the integers mod q, a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
(in the language of ring theory
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
X is the quotient of the univariate polynomial ring
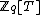 by the ideal generated by
by the ideal generated by 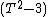 ). The multiplication operation in
). The multiplication operation in 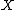 is defined by:
is defined by: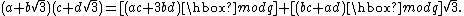
Since q > 2,
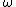 and
and 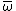 are in
are in 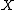 (in fact
(in fact 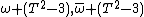 are in X, but by abuse of language we identify
are in X, but by abuse of language we identify 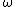 and
and 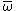 with their images in X under the natural ring homomorphism from
with their images in X under the natural ring homomorphism from 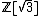 to X which sends the square root of 3 to T). Any product of two numbers in X is in X, but it's not a group
to X which sends the square root of 3 to T). Any product of two numbers in X is in X, but it's not a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication because not every element x has an inverse y such that xy = 1 (in fact X is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and the set of non-zero elements of X is a group if and only if
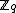 does not contain a square root of 3). If we consider only the elements that have inverses, we get a group X* of size at most
does not contain a square root of 3). If we consider only the elements that have inverses, we get a group X* of size at most 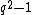 (since 0 has no inverse).
(since 0 has no inverse).Now, since
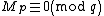 , and
, and 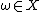 , we have
, we have 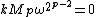 in X, which by equation (1) gives
in X, which by equation (1) gives 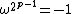 . Squaring both sides gives
. Squaring both sides gives 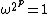 , showing that
, showing that 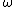 is invertible with inverse
is invertible with inverse 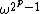 and so lies in X*, and moreover has an order
and so lies in X*, and moreover has an orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
dividing
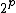 . In fact the order must equal
. In fact the order must equal 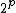 , since
, since 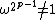 and so the order does not divide
and so the order does not divide 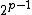 . Since the order of an element is at most the order (size) of the group, we conclude that
. Since the order of an element is at most the order (size) of the group, we conclude that 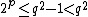 . But since q is the smallest prime factor of the composite
. But since q is the smallest prime factor of the composite 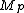 , we must have
, we must have 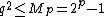 , yielding the contradiction
, yielding the contradiction 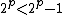 . So
. So 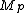 is prime.
is prime.Necessity
In the other direction, we suppose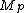 is prime and show
is prime and show 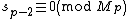 . We rely on a simplification of a proof by Öystein J. R.
. We rely on a simplification of a proof by Öystein J. R.Ödseth. First, notice that 3 is a quadratic non-residue mod Mp, since 2 p − 1 for odd p > 1 only takes on the value 7 mod 12, and so the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
properties tell us
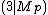 is −1. Euler's criterion
is −1. Euler's criterionEuler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
then gives us:
On the other hand, 2 is a quadratic residue mod
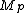 , since
, since 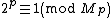 and so
and so 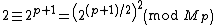 . Euler's criterion again gives:
. Euler's criterion again gives:Next, define
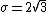 , and define X* similarly as before as the multiplicative group of
, and define X* similarly as before as the multiplicative group of 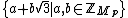 . We will use the following lemmas:
. We will use the following lemmas:(from Proofs of Fermat's little theorem#Proof using the binomial theorem)
for every integer a (Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
)
Then, in the group X* we have:
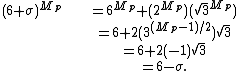
We chose
 such that
such that 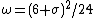 . Consequently, we can use this to compute
. Consequently, we can use this to compute 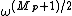 in the group X*:
in the group X*: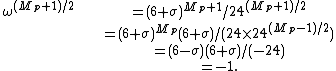
where we use the fact that
Since
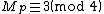 , all that remains is to multiply both sides of this equation by
, all that remains is to multiply both sides of this equation by 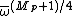 and use
and use 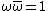 :
:-

Since sp−2 is an integer and is zero in X*, it is also zero mod Mp.
Applications
The Lucas–Lehmer test is the primality test used by the Great Internet Mersenne Prime SearchGreat Internet Mersenne Prime SearchThe Great Internet Mersenne Prime Search is a collaborative project of volunteers who use freely available computer software to search for Mersenne prime numbers. The project was founded by George Woltman, who also wrote the software Prime95 and MPrime for the project...
to locate large primes, and has been successful in locating many of the largest primes known to date. The test is considered valuable because it can provably test a very large number for primality within affordable time and, in contrast to the equivalently fast Pépin's testPépin's testIn mathematics, Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named for a French mathematician, Théophile Pépin.-Description of the test:...
for any Fermat number, can be tried on a large search space of numbers with the required form before reaching computational limits.
External links