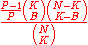Lottery mathematics
Encyclopedia
Lottery mathematics is used here to mean the calculation of the probabilities in a lottery
game. The lottery game used in the examples below is one in which one selects 6 numbers from 49, and hopes that as many of those 6 as possible match the 6 that are randomly selected from the same pool of 49 numbers in the "draw".
winner—this is true no matter in which order the numbers appear. The probability of this happening is 1 in 13,983,816.
This small chance
of winning can be demonstrated as follows:
Starting with a bag of 49 differently-numbered lottery balls, there are 49 different but equally likely ways of choosing the number of the first ball selected from the bag, and so there is a 1 in 49 chance of predicting
the number correctly. When the draw comes to the second number, there are now only 48 balls left in the bag (because the balls already drawn are not returned to the bag) so there is now a 1 in 48 chance of predicting this number.
Thus for each of the 49 ways of choosing the first number there are 48 different ways of choosing the second. This means that the probability
of correctly predicting 2 numbers drawn from 49 in the correct order is calculated as 1 in 49 × 48. On drawing the third number there are only 47 ways of choosing the number; but of course we could have got to this point in any of 49 × 48 ways, so the chances of correctly predicting 3 numbers drawn from 49, again in the correct order, is 1 in 49 × 48 × 47. This continues until the sixth number has been drawn, giving the final calculation, 49 × 48 × 47 × 46 × 45 × 44, which can also be written as . This works out to a very large number, 10,068,347,520, which is much bigger than the 14 million stated above.
. This works out to a very large number, 10,068,347,520, which is much bigger than the 14 million stated above.
The last step is to understand that the order of the 6 numbers is not significant. That is, if a ticket has the numbers 1, 2, 3, 4, 5, and 6, it wins as long as all the numbers 1 through 6 are drawn, no matter what order they come out in. Accordingly, given any set of 6 numbers, there are 6 × 5 × 4 × 3 × 2 × 1 = 6!
or 720 orders in which they could be drawn. Dividing 10,068,347,520 by 720 gives 13,983,816, also written as 49! / (6! × (49 - 6)!), or more generally as
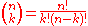 .
.
This function is called the combination
function; in a popular spreadsheet
computer program, this function is implemented as COMBIN(n, k). For example, COMBIN(49, 6) (the calculation shown above), would return 13,983,816. For the rest of this article, we will use the notation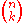 . "Combination" means the group of numbers selected, irrespective of the order in which they are drawn.
. "Combination" means the group of numbers selected, irrespective of the order in which they are drawn.
The range of possible combinations for a given lottery can be referred to as the "number space". "Coverage" is the percentage of a lottery's number space that is in play for a given drawing.
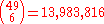 , as explained in the section above). The numerator equates to the number of ways one can select the winning numbers multiplied by the number of ways one can select the losing numbers.
, as explained in the section above). The numerator equates to the number of ways one can select the winning numbers multiplied by the number of ways one can select the losing numbers.
For a score of n (for example, if 3 of your numbers match the 6 balls drawn, then n = 3), there are ways of selecting n winning numbers from the 6 winning numbers. This means that there are 6 - n losing numbers, which are chosen from the 43 losing numbers in
ways of selecting n winning numbers from the 6 winning numbers. This means that there are 6 - n losing numbers, which are chosen from the 43 losing numbers in 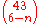 ways. The total number of combinations giving that result is, as stated above, the first number multiplied by the second. The expression is therefore
ways. The total number of combinations giving that result is, as stated above, the first number multiplied by the second. The expression is therefore  .
.
This can be written in a general form for all lotteries as:
 , where
, where  is the number of balls in lottery,
is the number of balls in lottery,  is the number of balls in a single ticket, and
is the number of balls in a single ticket, and  is the number of matching balls for a winning ticket.
is the number of matching balls for a winning ticket.
The generalisation of this formula is called the hypergeometric distribution (the HYPGEOMDIST function in most popular spreadsheets).
This gives the following results:
(or "bonus ball"). If the powerball is drawn from a pool of numbers different from the main lottery, then simply multiply the odds by the number of powerballs. For example, in the 6 from 49 lottery, if there were 10 powerball numbers, then the odds of getting a score of 3 and the powerball would be 1 in 56.66 × 10, or 566.6 (the probability would be divided by 10, to give an exact value of 8815/4994220). Another example of such a game is Mega Millions
, albeit with different jackpot odds.
Where more than 1 powerball is drawn from a separate pool of balls to the main lottery (for example, in the Euromillions
game), the odds of the different possible powerball matching scores should be calculated using the method shown in the "other scores" section above (in other words, treat the powerballs like a mini-lottery in their own right), and then multiplied by the odds of achieving the required main-lottery score.
If the powerball is drawn from the same pool of numbers as the main lottery, then, for a given target score, one must calculate the number of winning combinations, including the powerball. For games based on the Canadian lottery
(such as the United Kingdom
's lottery), after the 6 main balls are drawn, an extra ball is drawn from the same pool of balls, and this becomes the powerball (or "bonus ball"), and there is an extra prize for matching 5 balls and the bonus ball. As described in the "other scores" section above, the number of ways one can obtain a score of 5 from a single ticket is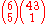 or 258. Since the number of remaining balls is 43, and the ticket has 1 unmatched number remaining, 1/43 of these 258 combinations will match the next ball drawn (the powerball). So, there are 258/43 = 6 ways of achieving it. Therefore, the odds of getting a score of 5 and the powerball are
or 258. Since the number of remaining balls is 43, and the ticket has 1 unmatched number remaining, 1/43 of these 258 combinations will match the next ball drawn (the powerball). So, there are 258/43 = 6 ways of achieving it. Therefore, the odds of getting a score of 5 and the powerball are  = 1 in 2,330,636.
= 1 in 2,330,636.
Of the 258 combinations that match 5 of the main 6 balls, in 42/43 of them the remaining number will not match the powerball, giving odds of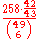 = 3/166,474 (approximately 55,491.33) for obtaining a score of 5 without matching the powerball.
= 3/166,474 (approximately 55,491.33) for obtaining a score of 5 without matching the powerball.
Using the same principle, to calculate the odds of getting a score of 2 and the powerball, calculate the number of ways to get a score of 2 as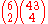 = 1,851,150 then multiply this by the probability of one of the remaining four numbers matching the bonus ball, which is 4/43. Since 1,851,150 × (4/43) = 172,200, the probability of obtaining the score of 2 and the bonus ball is
= 1,851,150 then multiply this by the probability of one of the remaining four numbers matching the bonus ball, which is 4/43. Since 1,851,150 × (4/43) = 172,200, the probability of obtaining the score of 2 and the bonus ball is  = 1025/83237. This gives approximate decimal odds of 81.2.
= 1025/83237. This gives approximate decimal odds of 81.2.
The general formula for matching balls in a
matching balls in a  choose
choose  lottery with one bonus ball from the
lottery with one bonus ball from the  pool of balls is:
pool of balls is:
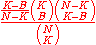
The general formula for matching balls in a
matching balls in a  choose
choose  lottery with zero bonus ball from the
lottery with zero bonus ball from the  pool of balls is:
pool of balls is:
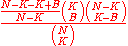
The general formula for matching balls in a
matching balls in a  choose
choose  lottery with one bonus ball from a separate pool of
lottery with one bonus ball from a separate pool of 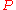 balls is:
balls is:
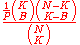
The general formula for matching balls in a
matching balls in a  choose
choose  lottery with no bonus ball from a separate pool of
lottery with no bonus ball from a separate pool of  balls is:
balls is:
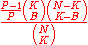
Lottery
A lottery is a form of gambling which involves the drawing of lots for a prize.Lottery is outlawed by some governments, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments...
game. The lottery game used in the examples below is one in which one selects 6 numbers from 49, and hopes that as many of those 6 as possible match the 6 that are randomly selected from the same pool of 49 numbers in the "draw".
Calculation explained in choosing 6 from 49
In a typical 6/49 game, six numbers are drawn from a range of 49 and if the six numbers on a ticket match the numbers drawn, the ticket holder is a jackpotProgressive jackpot
A progressive jackpot is a jackpot for a gaming machine where the value of the jackpot increases a small amount for every game played...
winner—this is true no matter in which order the numbers appear. The probability of this happening is 1 in 13,983,816.
This small chance
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of winning can be demonstrated as follows:
Starting with a bag of 49 differently-numbered lottery balls, there are 49 different but equally likely ways of choosing the number of the first ball selected from the bag, and so there is a 1 in 49 chance of predicting
Prediction
A prediction or forecast is a statement about the way things will happen in the future, often but not always based on experience or knowledge...
the number correctly. When the draw comes to the second number, there are now only 48 balls left in the bag (because the balls already drawn are not returned to the bag) so there is now a 1 in 48 chance of predicting this number.
Thus for each of the 49 ways of choosing the first number there are 48 different ways of choosing the second. This means that the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of correctly predicting 2 numbers drawn from 49 in the correct order is calculated as 1 in 49 × 48. On drawing the third number there are only 47 ways of choosing the number; but of course we could have got to this point in any of 49 × 48 ways, so the chances of correctly predicting 3 numbers drawn from 49, again in the correct order, is 1 in 49 × 48 × 47. This continues until the sixth number has been drawn, giving the final calculation, 49 × 48 × 47 × 46 × 45 × 44, which can also be written as
 . This works out to a very large number, 10,068,347,520, which is much bigger than the 14 million stated above.
. This works out to a very large number, 10,068,347,520, which is much bigger than the 14 million stated above.The last step is to understand that the order of the 6 numbers is not significant. That is, if a ticket has the numbers 1, 2, 3, 4, 5, and 6, it wins as long as all the numbers 1 through 6 are drawn, no matter what order they come out in. Accordingly, given any set of 6 numbers, there are 6 × 5 × 4 × 3 × 2 × 1 = 6!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
or 720 orders in which they could be drawn. Dividing 10,068,347,520 by 720 gives 13,983,816, also written as 49! / (6! × (49 - 6)!), or more generally as
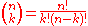 .
.This function is called the combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
function; in a popular spreadsheet
Spreadsheet
A spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
computer program, this function is implemented as COMBIN(n, k). For example, COMBIN(49, 6) (the calculation shown above), would return 13,983,816. For the rest of this article, we will use the notation
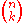 . "Combination" means the group of numbers selected, irrespective of the order in which they are drawn.
. "Combination" means the group of numbers selected, irrespective of the order in which they are drawn.The range of possible combinations for a given lottery can be referred to as the "number space". "Coverage" is the percentage of a lottery's number space that is in play for a given drawing.
Odds of getting other possibilities in choosing 6 from 49
One must divide the number of combinations producing the given result by the total number of possible combinations (for example,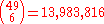 , as explained in the section above). The numerator equates to the number of ways one can select the winning numbers multiplied by the number of ways one can select the losing numbers.
, as explained in the section above). The numerator equates to the number of ways one can select the winning numbers multiplied by the number of ways one can select the losing numbers.For a score of n (for example, if 3 of your numbers match the 6 balls drawn, then n = 3), there are
 ways of selecting n winning numbers from the 6 winning numbers. This means that there are 6 - n losing numbers, which are chosen from the 43 losing numbers in
ways of selecting n winning numbers from the 6 winning numbers. This means that there are 6 - n losing numbers, which are chosen from the 43 losing numbers in 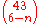 ways. The total number of combinations giving that result is, as stated above, the first number multiplied by the second. The expression is therefore
ways. The total number of combinations giving that result is, as stated above, the first number multiplied by the second. The expression is therefore  .
.This can be written in a general form for all lotteries as:
 , where
, where  is the number of balls in lottery,
is the number of balls in lottery,  is the number of balls in a single ticket, and
is the number of balls in a single ticket, and  is the number of matching balls for a winning ticket.
is the number of matching balls for a winning ticket.The generalisation of this formula is called the hypergeometric distribution (the HYPGEOMDIST function in most popular spreadsheets).
This gives the following results:
| Score | Calculation | Exact Probability | Approximate Decimal Probability | Approximate 1/Probability |
|---|---|---|---|---|
| 0 | 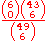 |
435,461/998,844 | 0.436 | 2.2938 |
| 1 | 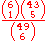 |
68,757/166,474 | 0.413 | 2.4212 |
| 2 |  |
44,075/332,948 | 0.132 | 7.5541 |
| 3 |  |
8,815/499,422 | 0.0177 | 56.66 |
| 4 | 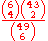 |
645/665,896 | 0.000969 | 1,032.4 |
| 5 | 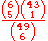 |
43/2,330,636 | 0.0000184 | 54,200.8 |
| 6 | 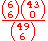 |
1/13,983,816 | 0.0000000715 | 13,983,816 |
Powerballs And Bonus Balls
Many lotteries have a powerballPowerball
Powerball is an American lottery game sold in 44 jurisdictions as a shared jackpot game. It is coordinated by the Multi-State Lottery Association , a non-profit organization formed by an agreement with lotteries. Powerball is a game whose advertised jackpot starts at $20 million and can roll into...
(or "bonus ball"). If the powerball is drawn from a pool of numbers different from the main lottery, then simply multiply the odds by the number of powerballs. For example, in the 6 from 49 lottery, if there were 10 powerball numbers, then the odds of getting a score of 3 and the powerball would be 1 in 56.66 × 10, or 566.6 (the probability would be divided by 10, to give an exact value of 8815/4994220). Another example of such a game is Mega Millions
Mega Millions
Mega Millions is a US multi-jurisdictional $1 lottery game. Since it replaced The Big Game in May 2002 , Mega Millions' advertised jackpots have started at $12 million, paid in 26 yearly installments , increasing when there is no jackpot winner...
, albeit with different jackpot odds.
Where more than 1 powerball is drawn from a separate pool of balls to the main lottery (for example, in the Euromillions
EuroMillions
EuroMillions is a transnational lottery, launched on 7 February 2004 by France's Française des Jeux, Spain's Loterías y Apuestas del Estado, and the United Kingdom's Camelot. The first draw was held on Friday 13 February 2004 in Paris...
game), the odds of the different possible powerball matching scores should be calculated using the method shown in the "other scores" section above (in other words, treat the powerballs like a mini-lottery in their own right), and then multiplied by the odds of achieving the required main-lottery score.
If the powerball is drawn from the same pool of numbers as the main lottery, then, for a given target score, one must calculate the number of winning combinations, including the powerball. For games based on the Canadian lottery
Lotto 6/49
Lotto 6/49 is one of Canada's two national lottery games. Winning numbers are drawn by the Interprovincial Lottery Corporation every Wednesday and Saturday. Launched on June 12, 1982, Lotto 6/49 was the first nationwide Canadian lottery game to allow players to choose their own numbers...
(such as the United Kingdom
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
's lottery), after the 6 main balls are drawn, an extra ball is drawn from the same pool of balls, and this becomes the powerball (or "bonus ball"), and there is an extra prize for matching 5 balls and the bonus ball. As described in the "other scores" section above, the number of ways one can obtain a score of 5 from a single ticket is
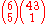 or 258. Since the number of remaining balls is 43, and the ticket has 1 unmatched number remaining, 1/43 of these 258 combinations will match the next ball drawn (the powerball). So, there are 258/43 = 6 ways of achieving it. Therefore, the odds of getting a score of 5 and the powerball are
or 258. Since the number of remaining balls is 43, and the ticket has 1 unmatched number remaining, 1/43 of these 258 combinations will match the next ball drawn (the powerball). So, there are 258/43 = 6 ways of achieving it. Therefore, the odds of getting a score of 5 and the powerball are  = 1 in 2,330,636.
= 1 in 2,330,636.Of the 258 combinations that match 5 of the main 6 balls, in 42/43 of them the remaining number will not match the powerball, giving odds of
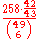 = 3/166,474 (approximately 55,491.33) for obtaining a score of 5 without matching the powerball.
= 3/166,474 (approximately 55,491.33) for obtaining a score of 5 without matching the powerball.Using the same principle, to calculate the odds of getting a score of 2 and the powerball, calculate the number of ways to get a score of 2 as
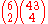 = 1,851,150 then multiply this by the probability of one of the remaining four numbers matching the bonus ball, which is 4/43. Since 1,851,150 × (4/43) = 172,200, the probability of obtaining the score of 2 and the bonus ball is
= 1,851,150 then multiply this by the probability of one of the remaining four numbers matching the bonus ball, which is 4/43. Since 1,851,150 × (4/43) = 172,200, the probability of obtaining the score of 2 and the bonus ball is  = 1025/83237. This gives approximate decimal odds of 81.2.
= 1025/83237. This gives approximate decimal odds of 81.2.The general formula for
 matching balls in a
matching balls in a  choose
choose  lottery with one bonus ball from the
lottery with one bonus ball from the  pool of balls is:
pool of balls is: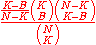
The general formula for
 matching balls in a
matching balls in a  choose
choose  lottery with zero bonus ball from the
lottery with zero bonus ball from the  pool of balls is:
pool of balls is: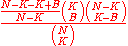
The general formula for
 matching balls in a
matching balls in a  choose
choose  lottery with one bonus ball from a separate pool of
lottery with one bonus ball from a separate pool of 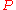 balls is:
balls is: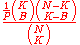
The general formula for
 matching balls in a
matching balls in a  choose
choose  lottery with no bonus ball from a separate pool of
lottery with no bonus ball from a separate pool of  balls is:
balls is: