
Loop entropy
Encyclopedia
Loop entropy is the entropy lost upon bringing together two residues of a polymer within a prescribed distance. For a single loop, the entropy varies logarithmically with the number of residues  in the loop
in the loop
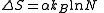
where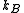 is Boltzmann's constant and
is Boltzmann's constant and  is a coefficient that depends on the properties of the polymer. This entropy formula corresponds to a power-law distribution
is a coefficient that depends on the properties of the polymer. This entropy formula corresponds to a power-law distribution  for the probability of the residues contacting.
for the probability of the residues contacting.
The loop entropy may also vary with the position of the contacting residues. Residues near the ends of the polymer are more likely to contact (quantitatively, have a lower ) than those in the middle (i.e., far from the ends), primarily due to excluded volume effects.
) than those in the middle (i.e., far from the ends), primarily due to excluded volume effects.
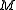 contacts among the residues,
contacts among the residues,
which define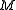 loops of the polymers. The Wang-Uhlenbeck matrix
loops of the polymers. The Wang-Uhlenbeck matrix 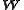 is an
is an  symmetric, real matrix whose elements
symmetric, real matrix whose elements  equal the number of common residues between loops
equal the number of common residues between loops  and
and  . The entropy of making the specified contacts equals
. The entropy of making the specified contacts equals
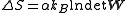
As an example, consider the entropy lost upon making the contacts between residues 26 and 84 and residues 58 and 110 in a polymer (cf. ribonuclease A
). The first and second loops have lengths 58 (=84-26) and 52 (=110-58), respectively, and they have 26 (=84-58) residues in common. The corresponding Wang-Uhlenbeck matrix is

whose determinant is 2340. Taking the logarithm and multiplying by the constants gives the entropy.
gives the entropy.
 in the loop
in the loop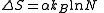
where
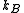 is Boltzmann's constant and
is Boltzmann's constant and  is a coefficient that depends on the properties of the polymer. This entropy formula corresponds to a power-law distribution
is a coefficient that depends on the properties of the polymer. This entropy formula corresponds to a power-law distribution  for the probability of the residues contacting.
for the probability of the residues contacting.The loop entropy may also vary with the position of the contacting residues. Residues near the ends of the polymer are more likely to contact (quantitatively, have a lower
 ) than those in the middle (i.e., far from the ends), primarily due to excluded volume effects.
) than those in the middle (i.e., far from the ends), primarily due to excluded volume effects.Wang-Uhlenbeck entropy
The loop entropy formula becomes more complicated with multiples loops, but may be determined for a Gaussian polymer using a matrix method developed by Wang and Uhlenbeck. Let there be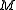 contacts among the residues,
contacts among the residues,which define
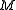 loops of the polymers. The Wang-Uhlenbeck matrix
loops of the polymers. The Wang-Uhlenbeck matrix 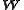 is an
is an  symmetric, real matrix whose elements
symmetric, real matrix whose elements  equal the number of common residues between loops
equal the number of common residues between loops  and
and  . The entropy of making the specified contacts equals
. The entropy of making the specified contacts equals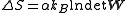
As an example, consider the entropy lost upon making the contacts between residues 26 and 84 and residues 58 and 110 in a polymer (cf. ribonuclease A
Ribonuclease A
Ribonuclease A is a pancreatic ribonuclease that cleaves single-stranded RNA. Bovine pancreatic RNase A is one of the classic model systems of protein science.-History:...
). The first and second loops have lengths 58 (=84-26) and 52 (=110-58), respectively, and they have 26 (=84-58) residues in common. The corresponding Wang-Uhlenbeck matrix is

whose determinant is 2340. Taking the logarithm and multiplying by the constants
 gives the entropy.
gives the entropy.

