Logical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional

Logical biconditional

In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...

 in propositional calculus

Propositional calculus

In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...

. It gives the functional

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 value true

True

True may refer to:* Truth, the state of being in accord with fact or reality-Music:* True , 1996* True , 2002* True , 1983** "True"...

if both functional arguments have the same logical value

Logical value

In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...

, and false

False

False or falsehood may refer to:*False *Lie or falsehood, a type of deception in the form of an untruthful statement*Falsity or falsehood, in law, deceitfulness by one party that results in damage to another...

if they are different.

It is customary practice in various applications, if not always technically precise, to indicate the operation of logical equality on the logical operands x and y by any of the following forms:



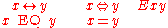
Some logicians, however, draw a firm distinction between a functional form, like those in the lefthand column, which they interpret as an application of a function to a pair of arguments — and thus a mere indication that the value of the compound expression depends on the values of the component expressions — and an equational form, like those in the righthand column, which they interpret as an assertion that the arguments have equal values, in other words, that the functional value of the compound expression is true.

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the plus sign "+" almost invariably indicates an operation that satisfies the axioms assigned to addition in the type of algebraic structure

Algebraic structure

In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...

 that is known as a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

.