
Loewner's torus inequality
Encyclopedia

Charles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
. It relates the systole and the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of an arbitrary Riemannian metric on the 2-torus.
Statement

Charles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
proved that every metric on the 2-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
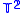 satisfies the optimal inequality
satisfies the optimal inequality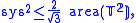
where "sys" is its systole, i.e. least length of a noncontractible loop. The constant appearing on the right hand side is the Hermite constant
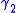 in dimension 2, so that Loewner's torus inequality can be rewritten as
in dimension 2, so that Loewner's torus inequality can be rewritten as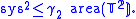
The inequality was first mentioned in the literature in .
Case of equality
The boundary case of equality is attained if and only if the metric is flat and homothetic to the so-called equilateral torus, i.e. torus whose group of deck transformations is precisely the hexagonal latticeHexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
spanned by the cube roots of unity in
 .
.Alternative formulation
Given a doubly periodic metric on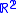 (e.g. an imbedding in
(e.g. an imbedding in 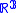 which is invariant by a
which is invariant by a 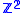 isometric action), there is a nonzero element
isometric action), there is a nonzero element  and a point
and a point 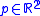 such that
such that  , where
, where  is a fundamental domain for the action, while
is a fundamental domain for the action, while 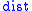 is the Riemannian distance, namely least length of a path joining
is the Riemannian distance, namely least length of a path joining  and
and  .
.Proof of Loewner's torus inequality
Loewner's torus inequality can be proved most easily by using the computational formula for the variance,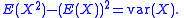
Namely, the formula is applied to the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
defined by the measure of the unit area flat torus in the conformal class of the given torus. For the random variable X, one takes the conformal factor of the given metric with respect to the flat one. Then the expected value E(X 2) of X 2 expresses the total area of the given metric. Meanwhile, the expected value E(X) of X can be related to the systole by using Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
. The variance of X can then be thought of as the isosystolic defect, analogous to the isoperimetric defect of Bonnesen's inequality
Bonnesen's inequality
Bonnesen's inequality is an inequality relating the length, the area, the radius of the incircle and the radius of the circumcircle of a Jordan curve. It is a strengthening of the classical isoperimetric inequality....
. This approach therefore produces the following version of Loewner's torus inequality with isosystolic defect:

where ƒ is the conformal factor of the metric with respect to a unit area flat metric in its conformal class.
Higher genus
Whether or not the inequality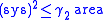
is satisfied by all surfaces of nonpositive Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
is unknown. For orientable surfaces of genus 2 and genus 20 and above, the answer is affirmative, see work by Katz and Sabourau below.
See also
- Pu's inequality for the real projective plane
- Gromov's systolic inequality for essential manifoldsGromov's systolic inequality for essential manifoldsIn the mathematical field of Riemannian geometry, M. Gromov's systolic inequality bounds the length of the shortest non-contractible loop on a Riemannian manifold in terms of the volume of the manifold...
- Gromov's inequality for complex projective space
- Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
(an example of a hexagonal lattice) - systoles of surfacesSystoles of surfacesIn mathematics, systolic inequalities for curves on surfaces were first studied by Charles Loewner in 1949 . Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to...

