Computational formula for the variance
Encyclopedia
In probability theory
and statistics
, the computational formula for the variance
Var(X) of a random variable
X is the formula
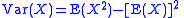
where E(X) is the expected value
of X.
A closely related identity can be used to calculate the sample variance, which is often used as an unbiased
estimate of the population variance:
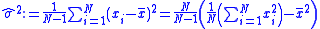
The second result is sometimes, unwisely, used in practice to calculate the variance. The problem is that subtracting two values having a similar value can lead to catastrophic cancellation.
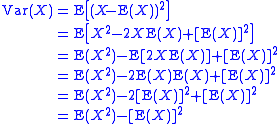
, with two random variables Xi and Xj:
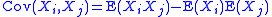
as well as for the n by n covariance matrix
of a random vector of length n:
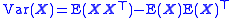
and for the n by m cross-covariance matrix between two random vectors of length n and m: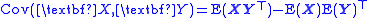
where expectations are taken element-wise and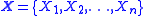
and 
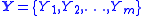are random vectors of respective lengths n and m.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the computational formula for the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
Var(X) of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is the formula
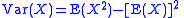
where E(X) is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of X.
A closely related identity can be used to calculate the sample variance, which is often used as an unbiased
Bias (statistics)
A statistic is biased if it is calculated in such a way that it is systematically different from the population parameter of interest. The following lists some types of, or aspects of, bias which should not be considered mutually exclusive:...
estimate of the population variance:
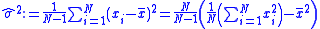
The second result is sometimes, unwisely, used in practice to calculate the variance. The problem is that subtracting two values having a similar value can lead to catastrophic cancellation.
Proof
The computational formula for the population variance follows in a straightforward manner from the linearity of expected values and the definition of variance: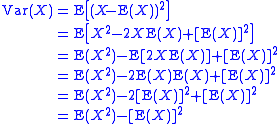Generalization to covariance
This formula can be generalized for covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
, with two random variables Xi and Xj:
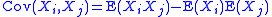
as well as for the n by n covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of a random vector of length n:
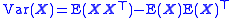
and for the n by m cross-covariance matrix between two random vectors of length n and m:
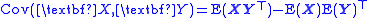
where expectations are taken element-wise 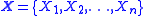and
and 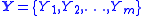are random vectors of respective lengths n and m.