Linear forms in logarithms
Encyclopedia
In number theory
the method of linear forms in logarithms is the application of estimates
for the magnitude of a finite sum
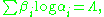
where the
and 
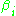are algebraic number
s. If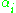
is a not a positive real number, then one has to allow log to denote some definite branch of the logarithm function in the complex plane. Applications include transcendence theory
, establishing measures of transcendence of real numbers, and the effective resolution of Diophantine equations. The theory of linear forms has been generalized to logarithms on elliptic curve
s and abelian varieties.
The class of results established by Alan Baker's work supply effective lower bounds for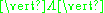
, in cases where 
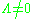. The lower bounds are in terms of quantities 
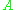and 
bounding, respectively, the heights of the 
and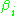 
. This work has many applications, in particular to the effective resolution of many types of diophantine equation
s.
An explicit result by Baker and Wüstholz
for a linear form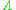
with integer coefficients yields a lower bound of the form
with a constant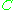
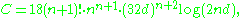
where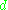
is the degree of the number field generated by the 
.
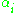Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
the method of linear forms in logarithms is the application of estimates
for the magnitude of a finite sum
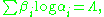
where the
and 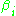are algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. If
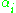is a not a positive real number, then one has to allow log to denote some definite branch of the logarithm function in the complex plane. Applications include transcendence theoryTranscendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
, establishing measures of transcendence of real numbers, and the effective resolution of Diophantine equations. The theory of linear forms has been generalized to logarithms on elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and abelian varieties.
The class of results established by Alan Baker's work supply effective lower bounds for
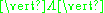, in cases where 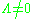. The lower bounds are in terms of quantities 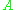and bounding, respectively, the heights of the and 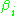. This work has many applications, in particular to the effective resolution of many types of diophantine equationDiophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s.
An explicit result by Baker and Wüstholz
Gisbert Wüstholz
Gisbert Wüstholz is a German mathematician who obtained his Ph.D. from the Albert Ludwigs University of Freiburg in 1977, under the supervision of Theodor Schneider. His contributions are mainly in the area of transcendental number theory and diophantine approximation...
for a linear form
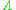with integer coefficients yields a lower bound of the formwith a constant
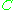
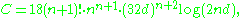
where
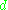is the degree of the number field generated by the .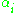