
Line-plane intersection
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the intersection of a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
and a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
can be the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
,
a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
, or
a line. Distinguishing these cases, and determining equations for the point and line in the latter cases have use, for example, in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, motion planning
Motion planning
Motion planning is a term used in robotics for the process of detailing a task into discrete motions....
, and collision detection
Collision detection
Collision detection typically refers to the computational problem of detecting the intersection of two or more objects. While the topic is most often associated with its use in video games and other physical simulations, it also has applications in robotics...
.
Parametric form
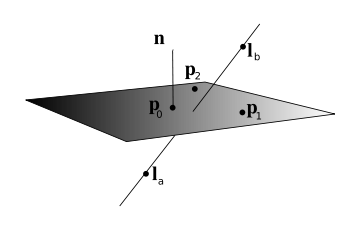
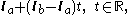
where
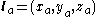 and
and 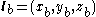
are two distinct points along the line.
Similarly a general point on a plane can be represented as
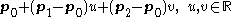
where
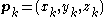 ,
,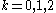 are three points in the plane which are not co-linear.
are three points in the plane which are not co-linear.The point at which the line intersects the plane is therefore described by setting the point on the line equal to the point on the plane, giving the parametric equation:
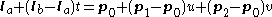
This can be simplified to
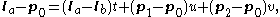
which can be expressed in matrix form as:
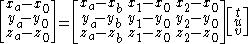
The point of intersection is then equal to
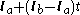
If the line is parallel to the plane then the vectors
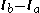 ,
, 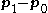 , and
, and 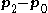 will be linearly dependent and the matrix will be singular. This situation will also occur when the line lies in the plane.
will be linearly dependent and the matrix will be singular. This situation will also occur when the line lies in the plane.If the solution satisfies the condition
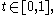 , then the intersection point is on the line between
, then the intersection point is on the line between 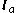 and
and 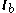 .
.If the solution satisfies

then the intersection point is in the plane inside the triangle spanned by the three points
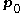 ,
, 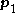 and
and 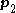 .
.This problem is typically solved by expressing it in matrix form, and inverting it:
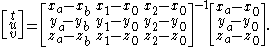
Algebraic form
In vector notationVector notation
This page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....
, a plane can be expressed as the set of points
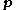 for which
for which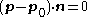
where
 is a normal vector to the plane and
is a normal vector to the plane and 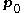 is a point on the plane.
is a point on the plane.The vector equation for a line is
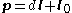
where
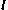 is a vector in the direction of the line and
is a vector in the direction of the line and 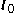 is a point on the line. Substitute the line into the plane equation to get
is a point on the line. Substitute the line into the plane equation to get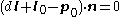
Distribute
 to get
to get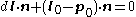
And solve for
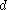
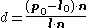
If the line starts outside the plane and is parallel to the plane, there is no intersection. In this case, the above denominator will be zero and the numerator will be non-zero. If the line starts inside the plane and is parallel to the plane, the line intersects the plane everywhere. In this case, both the numerator and denominator above will be zero. In all other cases, the line intersects the plane once and
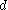 represents the intersection as the distance along the line from
represents the intersection as the distance along the line from 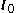 .
.Uses
In the ray tracing method of computer graphicsComputer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
a surface can be represented as a set of pieces of planes. The intersection of a ray of light with each plane is used to produce an image of the surface. In vision-based 3D reconstruction, a subfield of computer vision, depth values are commonly measured by so-called triangulation method, which finds the intersection between light plane and ray reflected toward camera.
The algorithm can be generalised to cover intersection with other planar figures, in particular, the intersection of a polyhedron with a line
Intersection of a polyhedron with a line
In computational geometry, the intersection of a polyhedron with a line is the problem of computing the intersection of a convex polyhedron and a ray in Euclidean space...
.

