
Lie product formula
Encyclopedia
In mathematics
, the Lie product formula, named for Sophus Lie
, states that for arbitrary n × n real
or complex
matrices
A and B,
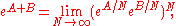
where eA denotes the matrix exponential
of A.
The Lie–Trotter product formula and the Trotter–Kato theorem extend this to certain unbounded linear operators A and B.
This formula is an analogue of the classical exponential law

which holds for all real or complex numbers x and y. If x and y are replaced with matrices A and B, and the exponential
replaced with a matrix exponential
, it is usually necessary for A and B to commute for the law to still hold. However, the Lie product formula holds for all matrices A and B, even ones which do not commute.
The formula has applications, for example, in the path integral formulation
of quantum mechanics. It allows one to separate the Schrödinger evolution operator into alternating increments of kinetic and potential operators. The same idea is used in the construction of splitting methods for the numerical solution of differential equation
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lie product formula, named for Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
, states that for arbitrary n × n real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A and B,
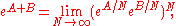
where eA denotes the matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of A.
The Lie–Trotter product formula and the Trotter–Kato theorem extend this to certain unbounded linear operators A and B.
This formula is an analogue of the classical exponential law

which holds for all real or complex numbers x and y. If x and y are replaced with matrices A and B, and the exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
replaced with a matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
, it is usually necessary for A and B to commute for the law to still hold. However, the Lie product formula holds for all matrices A and B, even ones which do not commute.
The formula has applications, for example, in the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics. It allows one to separate the Schrödinger evolution operator into alternating increments of kinetic and potential operators. The same idea is used in the construction of splitting methods for the numerical solution of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.

