Leray cover
Encyclopedia
In mathematics
, a Leray cover(ing) is a cover which allows for easy calculation of cohomology
.
Sheaf cohomology
measures the extent to which a locally exact sequence on a fixed topological space, for instance the deRham sequence, fails to be globally exact. Its definition, using derived functors, is reasonably natural, if technical. Moreover, important properties, such as the existence of a long exact sequence in cohomology corresponding to any short exact sequence of sheaves, follow directly from the definition. However, it is virtually impossible to calculate from the definition. On the other hand, Čech cohomology
with respect to an open cover is well-suited to calculation, but of limited usefulness because it depends on the open cover chosen, not only on the sheaves and the space. By taking a direct limit of Čech cohomology over arbitrarily fine covers, we obtain a Čech cohomology theory that does not depend on the open cover chosen. In reasonable circumstances (for instance, if the topological space is paracompact), the derived-functor cohomology agrees with this Ĉech cohomology obtained by direct limits. However, like the derived functor cohomology, this cover-independent Čech cohomology is virtually impossible to calculate from the definition. The Leray condition on an open cover ensures that the cover in question is already "fine enough." The derived functor cohomology agrees with the Čech cohomology with respect to any Leray cover.
Let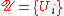
be an open cover of the topological space 
, and 
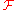a sheaf on X. We say that 
is a Leray cover with respect to 
if, for every finite set 
of indices, and for all 
, 
, in the derived functor cohomology. For example, if X is a separated scheme, and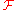 
is quasicoherent, then any cover of X by open affine subschemes is a Leray cover.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Leray cover(ing) is a cover which allows for easy calculation of cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
Sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
measures the extent to which a locally exact sequence on a fixed topological space, for instance the deRham sequence, fails to be globally exact. Its definition, using derived functors, is reasonably natural, if technical. Moreover, important properties, such as the existence of a long exact sequence in cohomology corresponding to any short exact sequence of sheaves, follow directly from the definition. However, it is virtually impossible to calculate from the definition. On the other hand, Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
with respect to an open cover is well-suited to calculation, but of limited usefulness because it depends on the open cover chosen, not only on the sheaves and the space. By taking a direct limit of Čech cohomology over arbitrarily fine covers, we obtain a Čech cohomology theory that does not depend on the open cover chosen. In reasonable circumstances (for instance, if the topological space is paracompact), the derived-functor cohomology agrees with this Ĉech cohomology obtained by direct limits. However, like the derived functor cohomology, this cover-independent Čech cohomology is virtually impossible to calculate from the definition. The Leray condition on an open cover ensures that the cover in question is already "fine enough." The derived functor cohomology agrees with the Čech cohomology with respect to any Leray cover.
Let
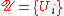be an open cover of the topological space , and 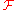a sheaf on X. We say that is a Leray cover with respect to if, for every finite set of indices, and for all , , in the derived functor cohomology. For example, if X is a separated scheme, and 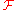is quasicoherent, then any cover of X by open affine subschemes is a Leray cover.