Leray's theorem
Encyclopedia
In algebraic geometry
, Leray's theorem relates abstract sheaf cohomology
with Čech cohomology
.
Let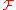
be a sheaf
on a topological space
and 
an open cover of 
If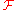 
is acyclic on every finite intersection of elements of 
, then
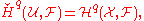
where
is the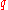 
-th Čech cohomology group of 
with respect to the open cover 
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Leray's theorem relates abstract sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
with Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
.
Let
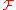be a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and an open cover of If 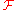is acyclic on every finite intersection of elements of , then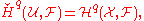where
is the 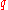-th Čech cohomology group of with respect to the open cover