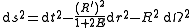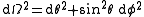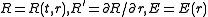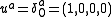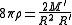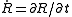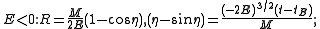Lemaitre-Tolman metric
Encyclopedia
The Lemaître–Tolman metric is the spherically symmetric dust solution of Einstein's field equations was first found by Lemaître
in 1933 and then Tolman in 1934. It was later investigated by Bondi
in 1947. This solution describes a spherical cloud of dust (finite or infinite) that is expanding or collapsing under gravity. It is also known as the Lemaître-Tolman-Bondi metric and the Tolman metric.
The metric is:
where:
The matter is comoving, which means its 4-velocity is:
so the spatial coordinates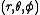 are attached to the particles of dust.
are attached to the particles of dust.
The pressure is zero (hence dust), the density is
and the evolution equation is
where
The evolution equation has three solutions, depending on the sign of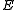 ,
,
which are known as hyperbolic, parabolic, and elliptic evolutions respectively.
The meanings of the three arbitrary functions, which depend on only, are:
only, are:
Special cases are the Schwarzschild metric
in geodesic coordinates
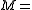 constant, and the Friedmann–Lemaître–Robertson–Walker metric, e.g.
constant, and the Friedmann–Lemaître–Robertson–Walker metric, e.g. 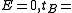 constant for the flat case.
constant for the flat case.
Georges Lemaître
Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
in 1933 and then Tolman in 1934. It was later investigated by Bondi
Hermann Bondi
Sir Hermann Bondi, KCB, FRS was an Anglo-Austrian mathematician and cosmologist. He is best known for developing the steady-state theory of the universe with Fred Hoyle and Thomas Gold as an alternative to the Big Bang theory, but his most lasting legacy will probably be his important...
in 1947. This solution describes a spherical cloud of dust (finite or infinite) that is expanding or collapsing under gravity. It is also known as the Lemaître-Tolman-Bondi metric and the Tolman metric.
The metric is:
where:
The matter is comoving, which means its 4-velocity is:
so the spatial coordinates
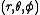 are attached to the particles of dust.
are attached to the particles of dust.The pressure is zero (hence dust), the density is
and the evolution equation is
where
The evolution equation has three solutions, depending on the sign of
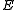 ,
,
which are known as hyperbolic, parabolic, and elliptic evolutions respectively.
The meanings of the three arbitrary functions, which depend on
 only, are:
only, are:
-
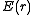 - both a local geometry parameter, and the energy per unit mass of the dust particles at comoving coordinate radius
- both a local geometry parameter, and the energy per unit mass of the dust particles at comoving coordinate radius  ,
, -
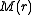 - the gravitational mass within the comoving sphere at radius
- the gravitational mass within the comoving sphere at radius  ,
, -
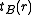 - the time of the big bang for worldlines at radius
- the time of the big bang for worldlines at radius  .
.
Special cases are the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
in geodesic coordinates
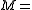 constant, and the Friedmann–Lemaître–Robertson–Walker metric, e.g.
constant, and the Friedmann–Lemaître–Robertson–Walker metric, e.g. 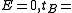 constant for the flat case.
constant for the flat case.