
Lebesgue spine
Encyclopedia
In mathematics
, in the area of potential theory
, a Lebesgue spine or Lebesgue thorn is a type of set used for discussing solutions to the Dirichlet problem
and related problems of potential theory. The Lebesgue spine was introduced in 1912 by Henri Lebesgue
to demonstrate that the Dirichlet problem does not always have a solution, particularly when the boundary has a sufficiently sharp edge protruding into the interior of the region.
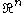 , for
, for 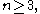 is defined as follows
is defined as follows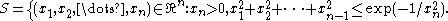
The important features of this set are that it is connected and path-connected in the euclidean topology
in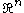 and the origin is a limit point
and the origin is a limit point
of the set, and yet the set is thin at the origin, as defined in the article Fine topology (potential theory)
.
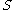 is not closed in the euclidean topology
is not closed in the euclidean topology
since it does not contain the origin which is a limit point
of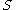 , but the set is closed in the fine topology
, but the set is closed in the fine topology
in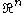 .
.
In comparison, it is not possible in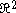 to construct such a connected set which is thin at the origin.
to construct such a connected set which is thin at the origin.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, a Lebesgue spine or Lebesgue thorn is a type of set used for discussing solutions to the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
and related problems of potential theory. The Lebesgue spine was introduced in 1912 by Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
to demonstrate that the Dirichlet problem does not always have a solution, particularly when the boundary has a sufficiently sharp edge protruding into the interior of the region.
Definition
A typical Lebesgue spine in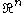 , for
, for 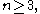 is defined as follows
is defined as follows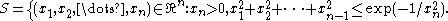
The important features of this set are that it is connected and path-connected in the euclidean topology
Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
in
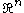 and the origin is a limit point
and the origin is a limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of the set, and yet the set is thin at the origin, as defined in the article Fine topology (potential theory)
Fine topology (potential theory)
In mathematics, in the field of potential theory, the fine topology is a natural topology for setting the study of subharmonic functions. In the earliest studies of subharmonic functions, only smooth functions were considered, namely those for which \Delta u \ge 0, where \Delta is the Laplacian...
.
Observations
The set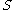 is not closed in the euclidean topology
is not closed in the euclidean topologyEuclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
since it does not contain the origin which is a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of
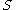 , but the set is closed in the fine topology
, but the set is closed in the fine topologyFine topology (potential theory)
In mathematics, in the field of potential theory, the fine topology is a natural topology for setting the study of subharmonic functions. In the earliest studies of subharmonic functions, only smooth functions were considered, namely those for which \Delta u \ge 0, where \Delta is the Laplacian...
in
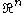 .
.In comparison, it is not possible in
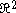 to construct such a connected set which is thin at the origin.
to construct such a connected set which is thin at the origin.

