Law of Truly Large Numbers
Encyclopedia
The law of truly large numbers, attributed to Persi Diaconis
and Frederick Mosteller, states that with a sample size large enough, any outrageous thing is likely to happen. Because we never find it notable when likely events occur, we highlight unlikely events and notice them more. The law seeks to debunk one element of supposed supernatural phenomenology.
In a sample of 1000 independent trials, the probability that the event does not happen in any of them is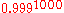
, or 36.8%. The probability that the event happens at least once in 1000 trials is then 1 − 0.368 = 0.632 or 63.2%. The probability that it happens at least once in 10,000 trials is 
.
This means that this "unlikely event" has a probability of 63.2% of happening if 1000 chances are given, or over 99.9% for 10,000 chances. In other words, a highly unlikely event, given enough tries, is even more unlikely to not occur.
and is sometimes called the Jeane Dixon effect (see also Postdiction
). It holds that the more predictions a psychic makes, the better the odds that one of them will "hit". Thus, if one comes true, the psychic expects us to forget the vast majority which did not happen.
Humans can be susceptible to this fallacy. A similar manifestation can be found in gambling
, where gamblers tend to remember their wins and forget their losses and thus hold an inflated view of their real winnings.
Steven Novella
describes this as the "lottery fallacy":
Persi Diaconis
Persi Warren Diaconis is an American mathematician and former professional magician. He is the Mary V. Sunseri Professor of Statistics and Mathematics at Stanford University....
and Frederick Mosteller, states that with a sample size large enough, any outrageous thing is likely to happen. Because we never find it notable when likely events occur, we highlight unlikely events and notice them more. The law seeks to debunk one element of supposed supernatural phenomenology.
Example
For a simplified example of the law, assume that a given event happens with a probability of 0.1% in one trial. Then the probability that this unlikely event does not happen in a single trial is 99.9% = 0.999.In a sample of 1000 independent trials, the probability that the event does not happen in any of them is
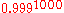, or 36.8%. The probability that the event happens at least once in 1000 trials is then 1 − 0.368 = 0.632 or 63.2%. The probability that it happens at least once in 10,000 trials is .This means that this "unlikely event" has a probability of 63.2% of happening if 1000 chances are given, or over 99.9% for 10,000 chances. In other words, a highly unlikely event, given enough tries, is even more unlikely to not occur.
In pseudoscience
The law comes up in pseudosciencePseudoscience
Pseudoscience is a claim, belief, or practice which is presented as scientific, but which does not adhere to a valid scientific method, lacks supporting evidence or plausibility, cannot be reliably tested, or otherwise lacks scientific status...
and is sometimes called the Jeane Dixon effect (see also Postdiction
Postdiction
According to critics of paranormal beliefs, postdiction is an effect of hindsight bias that explains claimed predictions of significant events, such as plane crashes and natural disasters...
). It holds that the more predictions a psychic makes, the better the odds that one of them will "hit". Thus, if one comes true, the psychic expects us to forget the vast majority which did not happen.
Humans can be susceptible to this fallacy. A similar manifestation can be found in gambling
Gambling
Gambling is the wagering of money or something of material value on an event with an uncertain outcome with the primary intent of winning additional money and/or material goods...
, where gamblers tend to remember their wins and forget their losses and thus hold an inflated view of their real winnings.
Steven Novella
Steven Novella
Steven P. Novella is an American clinical neurologist, assistant professor and Director of General Neurology at Yale University School of Medicine...
describes this as the "lottery fallacy":
It is also the lottery fallacy. If we hold a world-wide lottery and only one human in the 6.5 billion wins, the odds of that person winning is very small. But someone had to win. Chopra and Lanza are arguing that the winner could not have one by chance alone, because the odds were against it.
See also
- CoincidenceCoincidenceA coincidence is an event notable for its occurring in conjunction with other conditions, e.g. another event. As such, a coincidence occurs when something uncanny, accidental and unexpected happens under conditions named, but not under a defined relationship...
- Large numbersLarge numbersThis article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions...
- Law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
- Law of small numbersLaw of small numbersThe law of small numbers may refer to* The Law of Small Numbers , authored by Ladislaus Bortkiewicz** The Poisson distribution...
- Littlewood's lawLittlewood's lawLittlewood's Law states that individuals can expect a "miracle" to happen to them at the rate of about one per month.-History:The law was framed by Cambridge University Professor J. E...
- MiracleMiracleA miracle often denotes an event attributed to divine intervention. Alternatively, it may be an event attributed to a miracle worker, saint, or religious leader. A miracle is sometimes thought of as a perceptible interruption of the laws of nature. Others suggest that a god may work with the laws...
- Psychic phenomena
- Infinite monkey theoremInfinite monkey theoremThe infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare....