
Laver table
Encyclopedia
In mathematics
, Laver tables (named after Richard Laver
, who discovered them towards the end of the 1980s in connection with his works on set theory
) are tables of numbers that have certain properties.
n, one can define the n-th Laver table (with 2n rows and columns) by setting
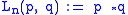 ,
,
where p denotes the row and q denotes the column of the entry. Define

and then calculate the remaining entries of each row from the m-th to the first using the equation
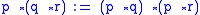
The resulting table is then called the n-th Laver table; for example, for n = 2, we have:
There is no known closed-form expression
to calculate the entries of a Laver table directly, and it is in fact suspected that such a formula does not exist.
(a large cardinal), it actually increases without bound. Nevertheless, it grows extremely slowly; Randall Dougherty showed that the first n for which the table entries' period can possibly be 32 is A(9,A(8,A(8,255))), where A denotes the Ackermann function
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Laver tables (named after Richard Laver
Richard Laver
Richard Laver is an American mathematician, working in set theory. He is a professor emeritus at the Department of Mathematics of the University of Colorado at Boulder.-His main results:Among Laver's notable achievements some are the following....
, who discovered them towards the end of the 1980s in connection with his works on set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
) are tables of numbers that have certain properties.
Definition
For a given a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, one can define the n-th Laver table (with 2n rows and columns) by setting
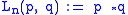 ,
,where p denotes the row and q denotes the column of the entry. Define

and then calculate the remaining entries of each row from the m-th to the first using the equation
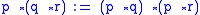
The resulting table is then called the n-th Laver table; for example, for n = 2, we have:
| 1 | 2 | 3 | 4 | |
| 1 | 2 | 4 | 2 | 4 |
| 2 | 3 | 4 | 3 | 4 |
| 3 | 4 | 4 | 4 | 4 |
| 4 | 1 | 2 | 3 | 4 |
There is no known closed-form expression
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
to calculate the entries of a Laver table directly, and it is in fact suspected that such a formula does not exist.
Periodicity
When looking at the first row of entries in a Laver table, it can be seen that the entries repeat with a certain periodicity m. This periodicity is always a power of 2; the first few periodicities are 1, 1, 2, 4, 4, 8, 8, 8, 8, 16, 16, ... . The sequence is increasing, and it was proved in 1995 by Richard Laver that under the assumption that there exists a rank-into-rankRank-into-rank
In set theory, a branch of mathematics, a rank-into-rank is a large cardinal λ satisfying one of the following four axioms :...
(a large cardinal), it actually increases without bound. Nevertheless, it grows extremely slowly; Randall Dougherty showed that the first n for which the table entries' period can possibly be 32 is A(9,A(8,A(8,255))), where A denotes the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
.
Further reading
- R. Laver, On the Algebra of Elementary Embeddings of a Rank into Itself, Advances in Mathematics 110, p. 334, 1995
- R. Dougherty, Critical Points in an Algebra of Elementary Embeddings, Annals of Pure and Applied Logic 65, p. 211, 1993
- Patrick Dehornoy, Diagrams colourings and applications, Proceedings of the East Asian School of Knots, Links and Related Topics, 2004 (online)

