Large deviations of Gaussian random functions
Encyclopedia
A random function – of either one variable (a random process), or two or more variables
(a random field
) – is called Gaussian if every finite-dimensional distribution
is a multivariate normal distribution. Gaussian random fields on the sphere
are useful (for example) when analysing
Sometimes, a value of a Gaussian random function deviates from its expected value
by several standard deviation
s. This is a large deviation. Though rare in a small domain (of space or/and time), large deviations may be quite usual in a large domain.
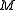be the maximal value of a Gaussian random function 
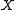on the
(two-dimensional) sphere. Assume that the expected value of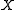
is 
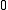(at every point of the sphere), and the standard deviation of 
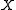is 
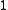(at every point of the sphere). Then, for large 
, 
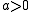is close to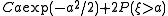 
,
where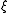
is distributed 
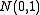(the standard normal distribution), and 
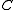is a constant; it does not depend on 
, but depends on the correlation function
of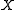
(see below). The relative error of the approximation decays exponentially for large 
.
The constant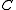
is easy to determine in the important special case described in terms of the directional derivative
of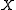
at a given point (of the sphere) in a given direction (tangential to the sphere). The derivative is random, with zero expectation and some standard deviation. The latter may depend on the point and the direction. However, if it does not depend, then it is equal to 
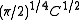(for the sphere of radius 
).
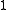The coefficient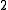
before 
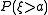is in fact the Euler characteristic
of the sphere (for the torus
it vanishes).
It is assumed that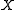
is twice continuously differentiable (almost surely
), and reaches its maximum at a single point (almost surely).
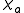of the set 
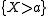of all points 
(of the sphere) such that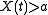 
. Its expected value (in other words, mean value) 
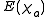can be calculated explicitly:
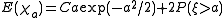
(which is far from being trivial, and involves Poincare–Hopf theorem, Gauss–Bonnet theorem, Rice formula etc).
The set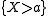
is the empty set
whenever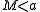
; in this case 
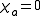. In the other case, when 
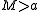, the set 
is non-empty; its Euler characteristic may take various values, depending on the topology of the set (the number of connected components
, and possible holes in these components). However, if
is large and 
then the set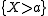 
is usually a small, slightly deformed disk or ellipse
(which is easy to guess, but quite difficult to prove). Thus, its Euler characteristic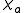
is usually equal to 
(given that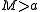 
). This is why 
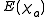is close to 
.
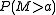(a random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
) – is called Gaussian if every finite-dimensional distribution
Finite-dimensional distribution
In mathematics, finite-dimensional distributions are a tool in the study of measures and stochastic processes. A lot of information can be gained by studying the "projection" of a measure onto a finite-dimensional vector space .-Finite-dimensional distributions of a measure:Let be a measure space...
is a multivariate normal distribution. Gaussian random fields on the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
are useful (for example) when analysing
- the anomalies in the cosmic microwave background radiationCosmic microwave background radiationIn cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
(see , pp. 8–9);
- brain images obtained by positron emission tomographyPositron emission tomographyPositron emission tomography is nuclear medicine imaging technique that produces a three-dimensional image or picture of functional processes in the body. The system detects pairs of gamma rays emitted indirectly by a positron-emitting radionuclide , which is introduced into the body on a...
(see , pp. 9–10).
Sometimes, a value of a Gaussian random function deviates from its expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
by several standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s. This is a large deviation. Though rare in a small domain (of space or/and time), large deviations may be quite usual in a large domain.
Basic statement
Let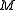 be the maximal value of a Gaussian random function 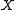on the(two-dimensional) sphere. Assume that the expected value of
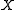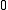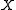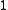is (at every point of the sphere), and the standard deviation of is (at every point of the sphere). Then, for large 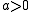, is close to 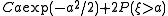,where
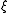is distributed 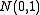(the standard normal distribution), and 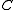is a constant; it does not depend on , but depends on the correlation functionCorrelation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
of
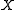(see below). The relative error of the approximation decays exponentially for large .The constant
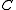is easy to determine in the important special case described in terms of the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of
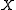at a given point (of the sphere) in a given direction (tangential to the sphere). The derivative is random, with zero expectation and some standard deviation. The latter may depend on the point and the direction. However, if it does not depend, then it is equal to 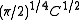(for the sphere of radius 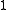).The coefficient
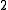before 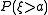is in fact the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the sphere (for the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
it vanishes).
It is assumed that
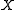is twice continuously differentiable (almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
), and reaches its maximum at a single point (almost surely).
The clue: mean Euler characteristic
The clue to the theory sketched above is, Euler characteristic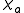 of the set 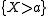of all points (of the sphere) such that 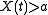. Its expected value (in other words, mean value) 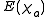can be calculated explicitly: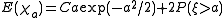(which is far from being trivial, and involves Poincare–Hopf theorem, Gauss–Bonnet theorem, Rice formula etc).
The set
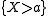is the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
whenever
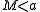; in this case 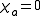. In the other case, when 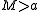, the set is non-empty; its Euler characteristic may take various values, depending on the topology of the set (the number of connected componentsConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, and possible holes in these components). However, if
is large and then the set 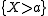is usually a small, slightly deformed disk or ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
(which is easy to guess, but quite difficult to prove). Thus, its Euler characteristic
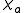is usually equal to (given that 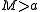). This is why 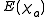is close to .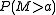