
Laplace principle (large deviations theory)
Encyclopedia
In mathematics
, Laplace's principle is a basic theorem
in large deviations theory
, similar to Varadhan's lemma
. It gives an asymptotic expression
for the Lebesgue integral
of exp(−θφ(x)) over a fixed set A as θ becomes large. Such expressions can be used, for example, in statistical mechanics
to determining the limiting behaviour of a system as the temperature tends to absolute zero
.
subset
of d-dimension
al Euclidean space
Rd and let φ : Rd → R be a measurable function
with
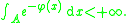
Then
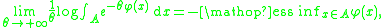
where ess inf denotes the essential infimum. Heuristically, this may be read as saying that for large θ,

s Pθ given by

to give an asymptotic expression for the probability of some set/event A as θ becomes large. For example, if X is a standard normally distributed random variable
on R, then
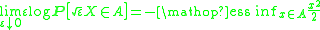
for every measurable set A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Laplace's principle is a basic theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
, similar to Varadhan's lemma
Varadhan's lemma
In mathematics, Varadhan's lemma is a result in large deviations theory named after S. R. Srinivasa Varadhan. The result gives information on the asymptotic distribution of a statistic φ of a family of random variables Zε as ε becomes small in terms of a rate function for the variables.-Statement...
. It gives an asymptotic expression
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
for the Lebesgue integral
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
of exp(−θφ(x)) over a fixed set A as θ becomes large. Such expressions can be used, for example, in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
to determining the limiting behaviour of a system as the temperature tends to absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
.
Statement of the result
Let A be a Lebesgue-measurableLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of d-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd and let φ : Rd → R be a measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
with
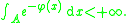
Then
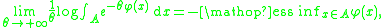
where ess inf denotes the essential infimum. Heuristically, this may be read as saying that for large θ,

Application
The Laplace principle can be applied to the family of probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s Pθ given by

to give an asymptotic expression for the probability of some set/event A as θ becomes large. For example, if X is a standard normally distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
on R, then
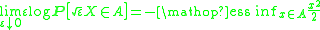
for every measurable set A.

