
Laplace limit
Encyclopedia
In mathematics, the Laplace limit is the maximum value of the eccentricity
for which the series solution to Kepler's equation converges. It is approximately
Kepler's equation
M = E − ε sin E relates the mean anomaly
M with the eccentric anomaly
E for a body moving in an ellipse
with eccentricity ε. This equation cannot be solved for E in terms of elementary functions, but the Lagrange reversion theorem
yields the solution as a power series in ε:
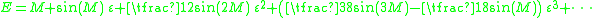
Laplace
realized that this series converges for small values of the eccentricity, but diverges when the eccentricity exceeds a certain value. The Laplace limit is this value. It is the radius of convergence
of the power series.
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
for which the series solution to Kepler's equation converges. It is approximately
- 0.66274 34193 49181 58097 47420 97109 25290.
Kepler's equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
M = E − ε sin E relates the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
M with the eccentric anomaly
Eccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
E for a body moving in an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
with eccentricity ε. This equation cannot be solved for E in terms of elementary functions, but the Lagrange reversion theorem
Lagrange reversion theorem
In mathematics, the Lagrange reversion theorem gives series or formal power series expansions of certain implicitly defined functions; indeed, of compositions with such functions....
yields the solution as a power series in ε:
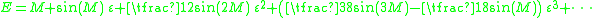
Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
realized that this series converges for small values of the eccentricity, but diverges when the eccentricity exceeds a certain value. The Laplace limit is this value. It is the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of the power series.

