
Landen's transformation
Encyclopedia
Landen
's transformation, independently rediscovered by Gauss
, is a mapping of the parameters of an elliptic integral
, which leaves the value of the integral unchanged.
In Gauss's formulation,
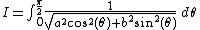
is unchanged if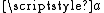 and
and 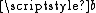 are replaced by their arithmetic
are replaced by their arithmetic
and geometric mean
s respectively, that is
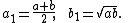
. It is convenient to first cast the integral in an algebraic
form by a substitution of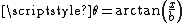 ,
, 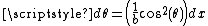 giving
giving
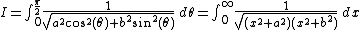
A further substitution of gives the desired result (in the algebraic form)
gives the desired result (in the algebraic form)
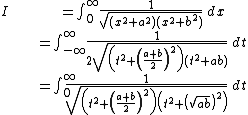
This latter step is facilitated by writing the radical as
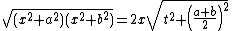
and the infinitesimal as
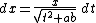
so that the factor of is easily recognized and cancelled between the two factors.
is easily recognized and cancelled between the two factors.
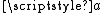 and
and 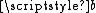 converge very rapidly to a common value, even if they are initially of different orders of magnitude. The limiting value is called the arithmetic-geometric mean of
converge very rapidly to a common value, even if they are initially of different orders of magnitude. The limiting value is called the arithmetic-geometric mean of 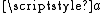 and
and 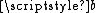 ,
,  . In the limit, the integrand becomes a constant, so that integration is trivial
. In the limit, the integrand becomes a constant, so that integration is trivial

The integral may also be recognized as a multiple of Legendre's complete elliptic integral of the first kind. Putting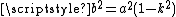
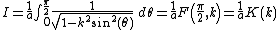
Hence, for any , the arithmetic-geometric mean and the complete elliptic integral of the first kind are related by
, the arithmetic-geometric mean and the complete elliptic integral of the first kind are related by
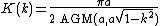
By performing an inverse transformation (reverse arithmetic-geometric mean iteration), that is
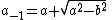
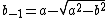

the relationship may be written as
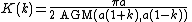
which may be solved for the AGM of a pair of arbitrary arguments;
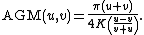
John Landen
John Landen was an English mathematician,He was born at Peakirk near Peterborough in Northamptonshire, and died at Milton in the same county...
's transformation, independently rediscovered by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, is a mapping of the parameters of an elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
, which leaves the value of the integral unchanged.
In Gauss's formulation,
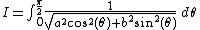
is unchanged if
 and
and  are replaced by their arithmetic
are replaced by their arithmeticArithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
and geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
s respectively, that is
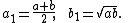
Proof
The transformation, may be achieved purely by integration by substitutionIntegration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
. It is convenient to first cast the integral in an algebraic
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
form by a substitution of
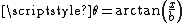 ,
, 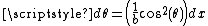 giving
giving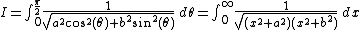
A further substitution of
 gives the desired result (in the algebraic form)
gives the desired result (in the algebraic form)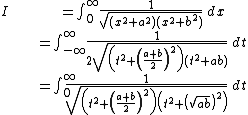
This latter step is facilitated by writing the radical as
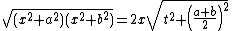
and the infinitesimal as
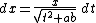
so that the factor of
 is easily recognized and cancelled between the two factors.
is easily recognized and cancelled between the two factors.Arithmetic-geometric mean and Legendre's first integral
If the transformation is iterated a number of times, then the parameters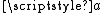 and
and 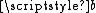 converge very rapidly to a common value, even if they are initially of different orders of magnitude. The limiting value is called the arithmetic-geometric mean of
converge very rapidly to a common value, even if they are initially of different orders of magnitude. The limiting value is called the arithmetic-geometric mean of 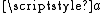 and
and 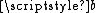 ,
,  . In the limit, the integrand becomes a constant, so that integration is trivial
. In the limit, the integrand becomes a constant, so that integration is trivial
The integral may also be recognized as a multiple of Legendre's complete elliptic integral of the first kind. Putting
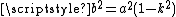
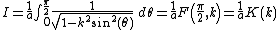
Hence, for any
 , the arithmetic-geometric mean and the complete elliptic integral of the first kind are related by
, the arithmetic-geometric mean and the complete elliptic integral of the first kind are related by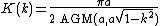
By performing an inverse transformation (reverse arithmetic-geometric mean iteration), that is
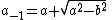
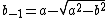

the relationship may be written as
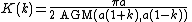
which may be solved for the AGM of a pair of arbitrary arguments;
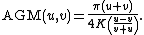
- The definition adopted here for
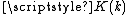 , differs from that used in the arithmetic-geometric mean article, such that
, differs from that used in the arithmetic-geometric mean article, such that 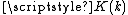 here is
here is 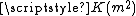 in that article.
in that article.

