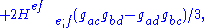Lanczos tensor
Encyclopedia
There are two different tensor
s sometimes referred to as the Lanczos tensor (both named after Cornelius Lanczos
):
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s sometimes referred to as the Lanczos tensor (both named after Cornelius Lanczos
Cornelius Lanczos
Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
):
- A tensor in the theory of quadratic Lagrangians, which vanishes in four dimensions.
- The potential tensor H for the Weyl tensorWeyl tensorIn differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
C, this can be expressed as:
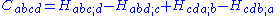
-
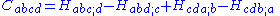
where the Lanczos tensor has the symmetries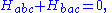
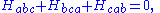
and where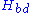 is defined by
is defined by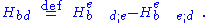
Thus, the Lanczos potential tensor is a gravitational fieldGravitational fieldThe gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
analog of
the vector potentialVector potentialIn vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
A for the electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
.
See also 'Introduction to 2-spinors in general relativity' (World Scientific, 2003) by Peter O'Donnell for a more detailed discussion of the Lanczos tensor and spinor.
External links
- http://www.worldscibooks.com/physics/5222.html Introduction to 2-spinors in general relativity
- gr-qc/9904006
-