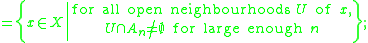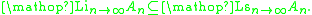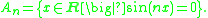Kuratowski convergence
Encyclopedia
In mathematics
, Kuratowski convergence is a notion of convergence
for sequences (or, more generally, nets
) of compact subsets
of metric space
s, named after the Polish
mathematician
Kazimierz Kuratowski
. Intuitively, the Kuratowski limit of a sequence of sets is where the sets "accumulate
".
. For any point x ∈ X and any non-empty compact subset A ⊆ X, let
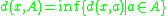 .
.
For any sequence of such subsets An ⊆ X, n ∈ N, the Kuratowski limit inferior (or lower closed limit) of An as n → ∞ is
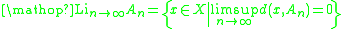
the Kuratowski limit superior (or upper closed limit) of An as n → ∞ is
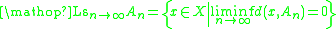
If the Kuratowski limits inferior and superior agree (i.e. are the same subset of X), then their common value is called the Kuratowski limit of the sets An as n → ∞ and denoted Ltn→∞An.
The definitions for a general net of compact subsets of X go through mutatis mutandis.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Kuratowski convergence is a notion of convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
for sequences (or, more generally, nets
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
) of compact subsets
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, named after the Polish
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
. Intuitively, the Kuratowski limit of a sequence of sets is where the sets "accumulate
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
".
Definitions
Let (X, d) be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. For any point x ∈ X and any non-empty compact subset A ⊆ X, let
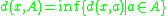 .
.For any sequence of such subsets An ⊆ X, n ∈ N, the Kuratowski limit inferior (or lower closed limit) of An as n → ∞ is
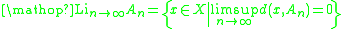
the Kuratowski limit superior (or upper closed limit) of An as n → ∞ is
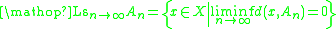
If the Kuratowski limits inferior and superior agree (i.e. are the same subset of X), then their common value is called the Kuratowski limit of the sets An as n → ∞ and denoted Ltn→∞An.
The definitions for a general net of compact subsets of X go through mutatis mutandis.
Properties
- Although it may seem counter-intuitive that the Kuratowski limit inferior involves the limit superior of the distances, and vice versa, the nomenclature becomes more obvious when one sees that, for any sequence of sets,
- I.e. the limit inferior is the smaller set and the limit superior the larger one.
- The terms upper and lower closed limit stem from the fact that Lin→∞An and Lsn→∞An are always closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s in the metric topology on (X, d).
Examples
- Let An be the zero set of sin(nx) as a function of x from R to itself
- Then An converges in the Kuratowski sense to the whole real line R.