
Kunita–Watanabe theorem
Encyclopedia
In stochastic calculus
, the Kunita-Watanabe theorem or Kunita-Watanabe inequality is a generalization of the Cauchy Schwarz inequality
to integrals of stochastic processes.
and H,K measurable processes. Then
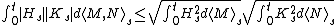
Where the brackets indicates the quadratic variation and quadratic covariation
operators. The integrals are understood in the Lebesgue-Stieltjes
sense.
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
, the Kunita-Watanabe theorem or Kunita-Watanabe inequality is a generalization of the Cauchy Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
to integrals of stochastic processes.
Statement of the Theorem
Let M, N be continuous local martingalesLocal martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
and H,K measurable processes. Then
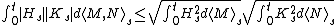
Where the brackets indicates the quadratic variation and quadratic covariation
Quadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
operators. The integrals are understood in the Lebesgue-Stieltjes
Lebesgue-Stieltjes integration
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework...
sense.

