Kullback's inequality
Encyclopedia
In information theory
and statistics
, Kullback's inequality is a lower bound on the Kullback–Leibler divergence
expressed in terms of the large deviations
rate function
. If P and Q are probability distribution
s on the real line, such that P is absolutely continuous with respect to Q, i.e. P<<Q, and whose first moments exist, then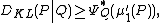
where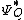
is the rate function, i.e. the convex conjugate
of the cumulant
-generating function, of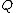
, and 
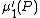is the first moment
of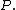
The Cramér–Rao bound is a corollary of this result.
s (measures) on the real line, whose first moments exist, and such that P<<Q. Consider the natural exponential family
of Q given by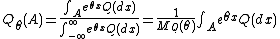
for every measurable set A, where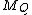
is the moment-generating function
of Q. (Note that Q0=Q.) Then
By Gibbs' inequality
we have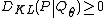
so that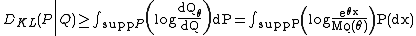
Simplifying the right side, we have, for every real θ where
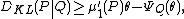
where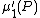
is the first moment, or mean, of P, and 
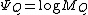is called the cumulant-generating function
. Taking the supremum completes the process of convex conjugation
and yields the rate function
:
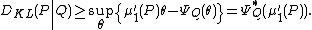
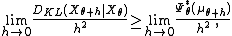
where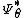
is the convex conjugate
of the cumulant-generating function
of
and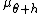 
is the first moment of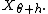 
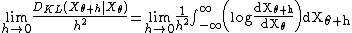
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Kullback's inequality is a lower bound on the Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
expressed in terms of the large deviations
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
. If P and Q are probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s on the real line, such that P is absolutely continuous with respect to Q, i.e. P<<Q, and whose first moments exist, then
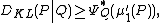
where
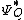is the rate function, i.e. the convex conjugateConvex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
of the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
-generating function, of
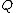, and 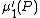is the first momentMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of
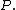
The Cramér–Rao bound is a corollary of this result.
Proof
Let P and Q be probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s (measures) on the real line, whose first moments exist, and such that P<<Q. Consider the natural exponential family
Natural exponential family
In probability and statistics, the natural exponential family is a class of probability distributions that is a special case of an exponential family...
of Q given by
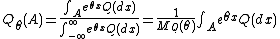
for every measurable set A, where
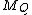is the moment-generating functionMoment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
of Q. (Note that Q0=Q.) Then
By Gibbs' inequality
Gibbs' inequality
In information theory, Gibbs' inequality is a statement about the mathematical entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality....
we have
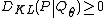so that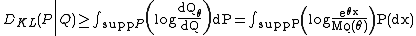Simplifying the right side, we have, for every real θ where
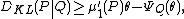
where
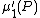is the first moment, or mean, of P, and 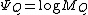is called the cumulant-generating functionCumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
. Taking the supremum completes the process of convex conjugation
Convex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
and yields the rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
:
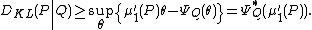
Start with Kullback's inequality
Let Xθ be a family of probability distributions on the real line indexed by the real parameter θ, and satisfying certain regularity conditions. Then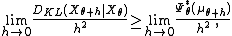where
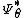is the convex conjugateConvex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
of the cumulant-generating function
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
of
and 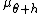is the first moment of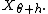 Left side
The left side of this inequality can be simplified as follows: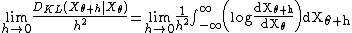
-
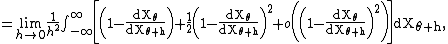
- where we have expanded the logarithm
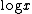in a Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in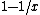
,
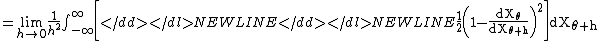
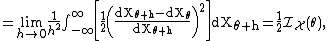
which is half the Fisher informationFisher informationIn mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
of the parameter θ.
Right side
The right side of the inequality can be developed as follows: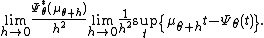
This supremum is attained at a value of t=τ where the first derivative of the cumulant-generating function is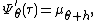
but we have 
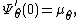so that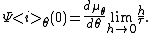
Moreover,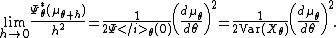
Putting both sides back together
We have:
which can be rearranged as: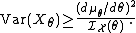
See also
- Kullback–Leibler divergenceKullback–Leibler divergenceIn probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
- Cramér–Rao bound
- Fisher informationFisher informationIn mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
- Large deviations theoryLarge deviations theoryIn probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
- Convex conjugateConvex conjugateIn mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
- Rate functionRate functionIn mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
- Moment-generating functionMoment-generating functionIn probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
- Kullback–Leibler divergence
- where we have expanded the logarithm