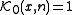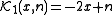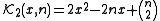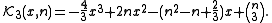Kravchuk polynomials
Encyclopedia
Kravchuk polynomials or Krawtchouk polynomials (and several other transliterations of the Ukrainian Кравчу́к) are discrete
orthogonal polynomials
associated with the binomial distribution, introduced by .
The first few polynomials are:
The Kravchuk polynomials are a special case of the Meixner polynomials of the first kind.
Discrete orthogonal polynomials
In mathematics, a sequence of discrete orthogonal polynomials is a sequence of polynomials that are pairwise orthogonal with repect to a discrete measure....
orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
associated with the binomial distribution, introduced by .
The first few polynomials are:
The Kravchuk polynomials are a special case of the Meixner polynomials of the first kind.
External links
- Krawtchouk Polynomials Home Page
- "Krawtchouk polynomial" at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...