
Kostant partition function
Encyclopedia
In representation theory
, the Kostant partition function, introduced by , of a root system
 is the number of ways one can represent a vector (weight
is the number of ways one can represent a vector (weight
) as an integral non-negative sum of the positive roots . Kostant used it to rewrite the Weyl character formula
. Kostant used it to rewrite the Weyl character formula
for the multiplicity
of a weight of an irreducible representation of a semisimple Lie algebra
.
The Kostant partition function can also be defined for Kac–Moody algebra
s and has similar properties.
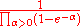
where the product is over all positive roots. Using Weyl's denominator formula
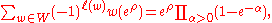
shows that the Weyl character formula
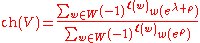
can also be written as
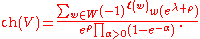
This allows the multiplicities of finite-dimensional irreducible representations in Weyl's character formula to be written as a finite sum involving values of the Kostant partition function, as these are the coefficients of the power series expansion of the denominator of the right hand side.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, the Kostant partition function, introduced by , of a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
 is the number of ways one can represent a vector (weight
is the number of ways one can represent a vector (weightWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
) as an integral non-negative sum of the positive roots
 . Kostant used it to rewrite the Weyl character formula
. Kostant used it to rewrite the Weyl character formulaWeyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
for the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of a weight of an irreducible representation of a semisimple Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
The Kostant partition function can also be defined for Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s and has similar properties.
Relation to the Weyl character formula
The values of Kostant's partition function are given by the coefficients of the power series expansion of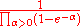
where the product is over all positive roots. Using Weyl's denominator formula
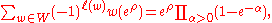
shows that the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
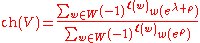
can also be written as
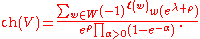
This allows the multiplicities of finite-dimensional irreducible representations in Weyl's character formula to be written as a finite sum involving values of the Kostant partition function, as these are the coefficients of the power series expansion of the denominator of the right hand side.

