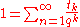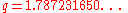Komornik–Loreti constant
Encyclopedia
The Komornik–Loreti constant is a mathematical constant
that represents the smallest number for which there still exists a unique q-development.
is called the q-expansion, or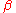
-expansion, of the positive real number x if, for all 
, 
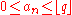, where 
is the floor function and 
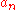need not be an integer. Any real number 
such that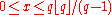 
has such an expansion, as can be found using the greedy algorithm
.
The special case of
, 
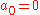, and 
or 1 is sometimes called a 
-development. 
gives the only 2-development. However, for almost all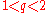 
, there are an infinite number of different 
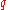-developments. Even more surprisingly though, there exist exceptional 
for which there exists only a single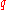 
-development. Furthermore, there is a smallest number 
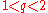known as the Komornik–Loreti constant for which there exists a unique 
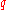-development.
The Komornik–Loreti constant is the value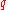
such that
where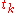
is the Thue–Morse sequence
, i.e.,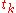
is the parity of the number of 1's in the binary representation of 
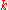. It has approximate value
The constant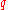
is also the unique positive real root of
This constant is transcendental
.
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
that represents the smallest number for which there still exists a unique q-development.
Definition
Given a real number q > 1, the series
is called the q-expansion, or
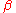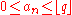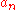-expansion, of the positive real number x if, for all , , where is the floor function and need not be an integer. Any real number such that 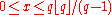has such an expansion, as can be found using the greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
.
The special case of
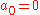, , and or 1 is sometimes called a -development. gives the only 2-development. However, for almost all 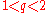, there are an infinite number of different 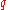-developments. Even more surprisingly though, there exist exceptional for which there exists only a single 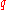-development. Furthermore, there is a smallest number 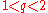known as the Komornik–Loreti constant for which there exists a unique 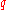-development.The Komornik–Loreti constant is the value
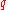such that
where
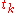is the Thue–Morse sequenceThue–Morse sequence
In mathematics, the Thue–Morse sequence, or Prouhet–Thue–Morse sequence, is a binary sequence that begins:Any other ordered pair of symbols may be used instead of 0 and 1; the logical structure of the Thue–Morse sequence does not depend on the symbols that are used to represent it.- Direct...
, i.e.,
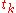is the parity of the number of 1's in the binary representation of 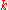. It has approximate value
The constant
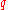is also the unique positive real root of
This constant is transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.