In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a Kochanek-Bartels spline or Kochanek-Bartels curve is a cubic Hermite spline

Cubic Hermite spline

In the mathematical subfield of numerical analysis a cubic Hermite spline , named in honor of Charles Hermite, is a third-degree spline with each polynomial of the spline in Hermite form...

 with tension, bias, and continuity parameters defined to change the behavior of the tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

s.

Given n + 1 knots

Spline (mathematics)

In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...

,

p₀, ..., p_n,

to be interpolated with n cubic Hermite curve segments, for each curve we have a starting point p_i and an ending point p_i+1 with starting tangent d_i and ending tangent d_i+1 defined by



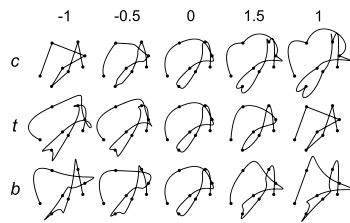
where t is the tension, b is the bias, and c is the continuity parameter.

The tension parameter, t, changes the length of the tangent vector. The bias parameter, b, primarily changes the direction of the tangent vector. The continuity parameter, c, changes the sharpness in change between tangents.

Setting each parameter to zero would give a Catmull-Rom spline.

The source code found here of Steve Noskowicz in 1996 actually describes the impact that each of these values has on the drawn curve:

Tension	T = +1-->Tight	T = −1--> Round
Bias	B = +1-->Post Shoot	B = −1--> Pre shoot
Continuity	C = +1-->Inverted corners	C = −1--> Box corners

The code includes matrix summary needed to generate these splines in a BASIC

BASIC

BASIC is a family of general-purpose, high-level programming languages whose design philosophy emphasizes ease of use - the name is an acronym from Beginner's All-purpose Symbolic Instruction Code....

dialect.