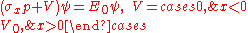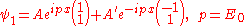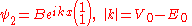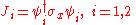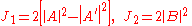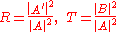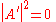Klein paradox
Encyclopedia
In 1929, physicist Oskar Klein
obtained a surprising result by applying the Dirac equation
to the familiar problem of electron scattering
from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping
. However, Klein’s result showed that if the potential is on the order of the electron mass, eV ~ mc², the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.
with energy 
and momentum 
.
The particle's wave function,
follows the time-independent Dirac equation
:
And
is the pauli matrix:
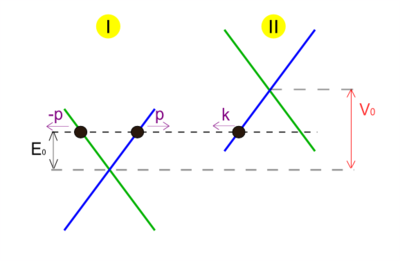Assuming the particle is propagating from the left, we obtain two solutions - one before the step, in region (1) and one under the potential, in region (2):
Where the coefficients A, A' and B are complex numbers.
Both the incoming and transmitted wave functions are associated with positive group velocity (Blue lines in Fig.1), whereas the reflected wave function is associated with negative group velocity. (Green lines in Fig.1)
We now want to calculate the transmission and reflection coefficients,
They are derived from the probability amplitude currents.
The definition of the probability current associated with the Dirac equation is:
In this case:
The transmission and reflection coefficients are:
Continuity of the wave function at
, yields:
And so the transmission coefficient is 1 and there is no reflection.
One interpretation of the paradox is that a potential step cannot reverse the direction of the group velocity of a massless relativistic particle. This explanation best suits the single particle solution cited above. Other, more complex interpretations are suggested in literature, in the context of quantum field theory
where the unrestrained tunnelling is shown to occur due to the existence of particle-antiparticle pairs at the potential.
The results are as surprising as in the massless case. The transmission coefficient is always larger than zero, and approaches 1 as the potential step goes to infinity.
These results were expanded to higher dimensions, and to other types of potentials, such as a linear step, a square barrier, etc.
Many experiments in electron transport in graphene
rely on the Klein paradox for massless particles.
Oskar Klein
Oskar Benjamin Klein was a Swedish theoretical physicist.Klein was born in Danderyd outside Stockholm, son of the chief rabbi of Stockholm, Dr. Gottlieb Klein from Homonna in Hungary and Antonie Levy...
obtained a surprising result by applying the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
to the familiar problem of electron scattering
Electron scattering
Electron scattering is the process whereby an electron is deflected from its original trajectory. As they are charged particles, they are subject to electromagnetic forces.-Phenomena:...
from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping
Damping
In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
. However, Klein’s result showed that if the potential is on the order of the electron mass, eV ~ mc², the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.
Massless particles
Consider a massless relativistic particle approaching a potential step of height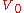 with energy and momentum 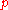.The particle's wave function,
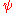follows the time-independent Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
:
And
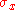is the pauli matrix:
Where the coefficients A, A' and B are complex numbers.
Both the incoming and transmitted wave functions are associated with positive group velocity (Blue lines in Fig.1), whereas the reflected wave function is associated with negative group velocity. (Green lines in Fig.1)
We now want to calculate the transmission and reflection coefficients,
They are derived from the probability amplitude currents.
The definition of the probability current associated with the Dirac equation is:
In this case:
The transmission and reflection coefficients are:
Continuity of the wave function at
, yields:
And so the transmission coefficient is 1 and there is no reflection.
One interpretation of the paradox is that a potential step cannot reverse the direction of the group velocity of a massless relativistic particle. This explanation best suits the single particle solution cited above. Other, more complex interpretations are suggested in literature, in the context of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where the unrestrained tunnelling is shown to occur due to the existence of particle-antiparticle pairs at the potential.
Other cases
For the massive case, the calculations are similar to the above.The results are as surprising as in the massless case. The transmission coefficient is always larger than zero, and approaches 1 as the potential step goes to infinity.
These results were expanded to higher dimensions, and to other types of potentials, such as a linear step, a square barrier, etc.
Many experiments in electron transport in graphene
Graphene
Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer...
rely on the Klein paradox for massless particles.