
Karamata's inequality
Encyclopedia
In mathematics
, Karamata's inequality, named after Jovan Karamata
, also known as the majorization inequality, is a theorem in elementary algebra
for convex and concave real-valued functions, defined on an interval of the real line. It generalizes the finite form of Jensen's inequality
.
 be an interval
be an interval
of the real line
and let denote a real-valued, convex function
denote a real-valued, convex function
defined on . If
. If  and
and  are numbers in
are numbers in 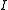 , such that
, such that  majorizes
majorizes 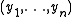 , then
, then
Here majorization means that
and, after relabeling the numbers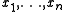 and
and 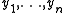 , respectively, in decreasing order, i.e.,
, respectively, in decreasing order, i.e.,
we have
If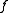 is a strictly convex function, then the inequality holds with equality if and only if, after relabeling according to , we have
is a strictly convex function, then the inequality holds with equality if and only if, after relabeling according to , we have  for all
for all 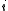 in
in 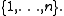
is a special case of this result. Consider the real numbers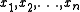 in
in 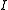 and let
and let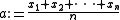
denote their arithmetic mean
. Then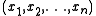 majorizes the
majorizes the  -tuple
-tuple  , since the arithmetic mean of the
, since the arithmetic mean of the 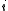 largest numbers of
largest numbers of  is at least as large as the arithmetic mean
is at least as large as the arithmetic mean  of all the
of all the  numbers, for every
numbers, for every 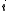 in
in 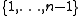 . By Karamata's inequality for the convex function
. By Karamata's inequality for the convex function  ,
,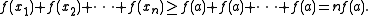
Dividing by gives Jensen's inequality. The sign is reversed if
gives Jensen's inequality. The sign is reversed if 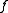 is concave.
is concave.
If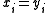 for all
for all 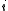 in
in 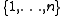 , then the inequality holds with equality, hence we may assume in the following that
, then the inequality holds with equality, hence we may assume in the following that 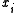 ≠
≠  for at least one
for at least one 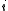 .
.
If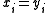 for an
for an 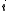 in
in  , then the inequality and the majorization properties , are not affected if we remove
, then the inequality and the majorization properties , are not affected if we remove 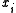 and
and 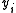 . Hence we may assume that
. Hence we may assume that  ≠
≠ 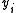 for all
for all 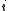 in
in 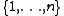 .
.
It's a property of convex functions that for two numbers ≠
≠ 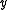 in the interval
in the interval 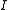 the slope
the slope
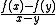
of the secant line
through the points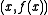 and
and 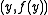 of the graph
of the graph
of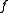 is a monotonically non-decreasing function in
is a monotonically non-decreasing function in  for
for 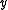 fixed (and vice versa). This implies that
fixed (and vice versa). This implies that
for all in
in 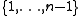 . Define
. Define  and
and

for all in
in 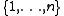 . By the majorization property ,
. By the majorization property , 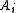 ≥
≥  for all
for all  in
in 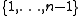 and by ,
and by , 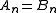 . Hence,
. Hence,
which proves Karamata's inequality .
To discuss the case of equality in , note that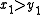 by and our assumption
by and our assumption 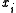 ≠
≠  for all
for all 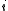 in
in 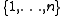 . Let
. Let 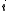 be the smallest index such that
be the smallest index such that  ≠
≠ 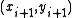 , which exists due to . Then
, which exists due to . Then 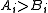 . If
. If  is strictly convex, then there is strict inequality in , meaning that
is strictly convex, then there is strict inequality in , meaning that  . Hence there is a strictly positive term in the sum on the right hand side of and equality in cannot hold.
. Hence there is a strictly positive term in the sum on the right hand side of and equality in cannot hold.
If the convex function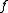 is non-decreasing, then
is non-decreasing, then 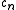 ≥
≥ 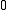 . The relaxed condition means that
. The relaxed condition means that 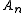 ≥
≥ 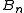 , which is enough to conclude that
, which is enough to conclude that 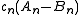 ≥
≥ 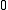 in the last step of .
in the last step of .
If the function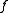 is strictly convex and non-decreasing, then
is strictly convex and non-decreasing, then  . It only remains to discuss the case
. It only remains to discuss the case 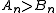 . However, then there is a strictly positive term on the right hand side of and equality in cannot hold.
. However, then there is a strictly positive term on the right hand side of and equality in cannot hold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Karamata's inequality, named after Jovan Karamata
Jovan Karamata
Jovan Karamata was one of the greatest Serbian mathematicians of the 20th century. He is remembered for contributions to analysis, in particular, the Tauberian theory and the theory of slowly varying functions...
, also known as the majorization inequality, is a theorem in elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
for convex and concave real-valued functions, defined on an interval of the real line. It generalizes the finite form of Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
.
Statement of the inequatlity
Let be an interval
be an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and let
 denote a real-valued, convex function
denote a real-valued, convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
defined on
 . If
. If  and
and  are numbers in
are numbers in 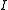 , such that
, such that  majorizes
majorizes 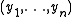 , then
, thenHere majorization means that
and, after relabeling the numbers
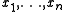 and
and 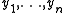 , respectively, in decreasing order, i.e.,
, respectively, in decreasing order, i.e.,we have
If
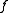 is a strictly convex function, then the inequality holds with equality if and only if, after relabeling according to , we have
is a strictly convex function, then the inequality holds with equality if and only if, after relabeling according to , we have  for all
for all 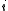 in
in 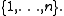
Remarks
- If the convex function
 is non-decreasing, then the proof of below and the discussion of equality in case of strict convexity shows that the equality can be relaxed to
is non-decreasing, then the proof of below and the discussion of equality in case of strict convexity shows that the equality can be relaxed to
- The inequality is reversed if
 is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
, since in this case the function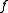 is convex.
is convex.
Example
The finite form of Jensen's inequalityJensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
is a special case of this result. Consider the real numbers
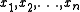 in
in 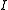 and let
and let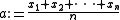
denote their arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
. Then
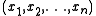 majorizes the
majorizes the  -tuple
-tuple  , since the arithmetic mean of the
, since the arithmetic mean of the 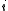 largest numbers of
largest numbers of  is at least as large as the arithmetic mean
is at least as large as the arithmetic mean  of all the
of all the  numbers, for every
numbers, for every 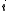 in
in 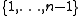 . By Karamata's inequality for the convex function
. By Karamata's inequality for the convex function  ,
,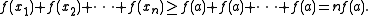
Dividing by
 gives Jensen's inequality. The sign is reversed if
gives Jensen's inequality. The sign is reversed if 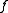 is concave.
is concave.Proof of the inequality
We may assume that the numbers are in decreasing order as specified in .If
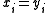 for all
for all 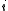 in
in 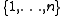 , then the inequality holds with equality, hence we may assume in the following that
, then the inequality holds with equality, hence we may assume in the following that 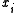 ≠
≠  for at least one
for at least one 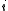 .
.If
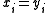 for an
for an 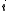 in
in  , then the inequality and the majorization properties , are not affected if we remove
, then the inequality and the majorization properties , are not affected if we remove 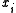 and
and 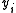 . Hence we may assume that
. Hence we may assume that  ≠
≠ 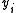 for all
for all 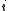 in
in 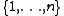 .
.It's a property of convex functions that for two numbers
 ≠
≠ 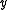 in the interval
in the interval 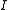 the slope
the slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
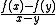
of the secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
through the points
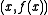 and
and 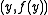 of the graph
of the graphGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of
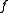 is a monotonically non-decreasing function in
is a monotonically non-decreasing function in  for
for 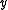 fixed (and vice versa). This implies that
fixed (and vice versa). This implies thatfor all
 in
in 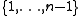 . Define
. Define  and
and
for all
 in
in 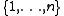 . By the majorization property ,
. By the majorization property , 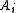 ≥
≥  for all
for all  in
in 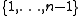 and by ,
and by , 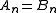 . Hence,
. Hence,which proves Karamata's inequality .
To discuss the case of equality in , note that
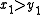 by and our assumption
by and our assumption 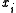 ≠
≠  for all
for all 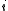 in
in 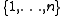 . Let
. Let 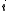 be the smallest index such that
be the smallest index such that  ≠
≠ 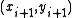 , which exists due to . Then
, which exists due to . Then 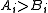 . If
. If  is strictly convex, then there is strict inequality in , meaning that
is strictly convex, then there is strict inequality in , meaning that  . Hence there is a strictly positive term in the sum on the right hand side of and equality in cannot hold.
. Hence there is a strictly positive term in the sum on the right hand side of and equality in cannot hold.If the convex function
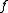 is non-decreasing, then
is non-decreasing, then 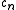 ≥
≥ 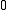 . The relaxed condition means that
. The relaxed condition means that 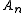 ≥
≥ 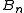 , which is enough to conclude that
, which is enough to conclude that 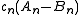 ≥
≥ 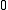 in the last step of .
in the last step of .If the function
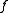 is strictly convex and non-decreasing, then
is strictly convex and non-decreasing, then  . It only remains to discuss the case
. It only remains to discuss the case 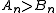 . However, then there is a strictly positive term on the right hand side of and equality in cannot hold.
. However, then there is a strictly positive term on the right hand side of and equality in cannot hold.
