Item tree analysis
Encyclopedia
Item tree analysis is a data analytical
method which allows constructing a
hierarchical structure on the items of a questionnaire
or test
from observed response
patterns.
Assume that we have a questionnaire with m items and that subjects can
answer positive (1) or negative (0) to each of these items, i.e. the items are
dichotomous
. If n subjects answer the items this results in a binary
data matrix
D
with m columns and n rows.
Typical examples of this data format are test items which can be solved (1) or failed
(0) by subjects. Other typical examples are questionnaires where the items are
statements to which subjects can agree (1) or disagree (0).
Depending on the content of the items it is possible that the response of a subject to an
item j determines her or his responses to other items. It is, for example, possible that
each subject who agrees to item j will also agree to item i. In this case we say that
item j implies item i (short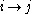
). The goal of an ITA is to uncover such
deterministic implications from the data set
D.
,
which we refer in the following as Classical ITA, is a logically consistent set of
implications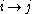
. Logically consistent means that if i implies j and j implies k then i implies k for each triple i, j, k of items. Thus the outcome of an ITA is a reflexive
and transitive
relation on the item set, i.e. a quasi-order on the items.
A different algorithm to perform an ITA was suggested in Schrepp (1999). This algorithm is called Inductive ITA.
Classical ITA and inductive ITA both construct a quasi-order on the item set by explorative data analysis
. But both methods use a different algorithm to construct this quasi-order. For a given data set the resulting quasi-orders from classical and inductive ITA will usually differ.
A detailed description of the algorithms used in classical and inductive ITA can be found in Schrepp (2003) or Schrepp (2006)http://www.jstatsoft.org/v16/i10/paper. In a recent paper (Sargin & Ünlü, 2009) some modifications to the algorithm of inductive ITA are proposed, which improve the ability of this method to detect the correct implications from data (especially in the case of higher random response error rates).
Boolean analysis
was introduced by Flament in 1976. The goal of a Boolean analysis is to
detect deterministic dependencies (formulas from Boolean logic
connecting the items, like for example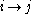
, 
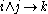, and 
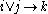) between the items of a questionnaire or test.
Since the basic work of Flament (1976) a number of different methods for boolean analysis
have been developed. See, for example, Van Buggenhaut and Degreef (1987), Duquenne (1987) or Theuns (1994).
These methods share the goal to derive
deterministic dependencies between the items of a
questionnaire from data, but differ in the algorithms to reach this goal. A comparison of ITA
to other methods of boolean data analysis can be found in Schrepp (2003).
Held and Korossy (1998) analyzes implications on a set of algebra
problems with classical ITA. Item tree analysis is also used in a number of social science studies
to get insight
into the structure of dichotomous data. In Bart and Krus (1973), for example, a predecessor of ITA is used to establish a hierarchical order on items that describe socially unaccepted behavior. In Janssens (1999) a method of Boolean analysis is used to investigate the
integration process of minorities
into the value system
of the dominant culture. Schrepp describes several applications of inductive ITA in the analysis of dependencies between items of social science questionnaires.
The ISSSP is a continuing annual program of cross-national collaboration on surveys covering important topics for social science research. The program conducts each year one survey with comparable questions in each of the participating nations. The theme of the 1995 survey was national identity
. We analyze the results for question 4 for the data set of Western Germany
.
The statement for question 4 was:
Some people say the following things are important for being truly German. Others say they are not important. How important do you think each of the following is:
1. to have been born in Germany
2. to have German citizenship
3. to have lived in Germany for most of one’s life
4. to be able to speak German
5. to be a Christian
6. to respect Germany’s political institutions
7. to feel German
The subjects had the response possibilities Very important, Important, Not very important, Not important at all, and Can’t choose to answer the statements.
To apply ITA to this data set we changed the answer categories.
Very important and Important are coded as 1. Not very important and Not important at all are coded as 0. Can’t choose was handled as missing data.
The following figure shows the resulting quasi-orders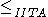
from inductive ITA and 
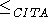from classical ITA.
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
method which allows constructing a
hierarchical structure on the items of a questionnaire
Questionnaire
A questionnaire is a research instrument consisting of a series of questions and other prompts for the purpose of gathering information from respondents. Although they are often designed for statistical analysis of the responses, this is not always the case...
or test
Concept inventory
A concept inventory is a criterion-referenced test designed to evaluate whether a student has an accurate working knowledge of a specific set of concepts. To ensure interpretability, it is common to have multiple items that address a single idea...
from observed response
patterns.
Assume that we have a questionnaire with m items and that subjects can
answer positive (1) or negative (0) to each of these items, i.e. the items are
dichotomous
Dichotomy
A dichotomy is any splitting of a whole into exactly two non-overlapping parts, meaning it is a procedure in which a whole is divided into two parts...
. If n subjects answer the items this results in a binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
data matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
D
with m columns and n rows.
Typical examples of this data format are test items which can be solved (1) or failed
(0) by subjects. Other typical examples are questionnaires where the items are
statements to which subjects can agree (1) or disagree (0).
Depending on the content of the items it is possible that the response of a subject to an
item j determines her or his responses to other items. It is, for example, possible that
each subject who agrees to item j will also agree to item i. In this case we say that
item j implies item i (short
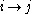). The goal of an ITA is to uncover suchdeterministic implications from the data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
D.
Algorithms for ITA
ITA was originally developed by Van Leeuwe in 1974. The result of his algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
,
which we refer in the following as Classical ITA, is a logically consistent set of
implications
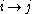. Logically consistent means that if i implies j and j implies k then i implies k for each triple i, j, k of items. Thus the outcome of an ITA is a reflexiveReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
relation on the item set, i.e. a quasi-order on the items.
A different algorithm to perform an ITA was suggested in Schrepp (1999). This algorithm is called Inductive ITA.
Classical ITA and inductive ITA both construct a quasi-order on the item set by explorative data analysis
Exploratory data analysis
In statistics, exploratory data analysis is an approach to analysing data sets to summarize their main characteristics in easy-to-understand form, often with visual graphs, without using a statistical model or having formulated a hypothesis...
. But both methods use a different algorithm to construct this quasi-order. For a given data set the resulting quasi-orders from classical and inductive ITA will usually differ.
A detailed description of the algorithms used in classical and inductive ITA can be found in Schrepp (2003) or Schrepp (2006)http://www.jstatsoft.org/v16/i10/paper. In a recent paper (Sargin & Ünlü, 2009) some modifications to the algorithm of inductive ITA are proposed, which improve the ability of this method to detect the correct implications from data (especially in the case of higher random response error rates).
Relation to other methods
ITA belongs to a group of data analysis methods called Boolean analysis of questionnaires.Boolean analysis
Boolean analysis
Boolean analysis was introduced by Flament . The goal of a Boolean analysis is to detect deterministic dependencies between the items of a questionnaire or similar data-structures in observed response patterns. These deterministic dependencies have the form of logical formulas connecting the items...
was introduced by Flament in 1976. The goal of a Boolean analysis is to
detect deterministic dependencies (formulas from Boolean logic
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
connecting the items, like for example
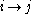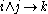, , and 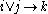) between the items of a questionnaire or test.Since the basic work of Flament (1976) a number of different methods for boolean analysis
have been developed. See, for example, Van Buggenhaut and Degreef (1987), Duquenne (1987) or Theuns (1994).
These methods share the goal to derive
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
deterministic dependencies between the items of a
questionnaire from data, but differ in the algorithms to reach this goal. A comparison of ITA
to other methods of boolean data analysis can be found in Schrepp (2003).
Applications
There are several research papers available, which describe concrete applications of item tree analysis.Held and Korossy (1998) analyzes implications on a set of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
problems with classical ITA. Item tree analysis is also used in a number of social science studies
Social studies
Social studies is the "integrated study of the social sciences and humanities to promote civic competence," as defined by the American National Council for the Social Studies...
to get insight
Insight
Insight is the understanding of a specific cause and effect in a specific context. Insight can be used with several related meanings:*a piece of information...
into the structure of dichotomous data. In Bart and Krus (1973), for example, a predecessor of ITA is used to establish a hierarchical order on items that describe socially unaccepted behavior. In Janssens (1999) a method of Boolean analysis is used to investigate the
integration process of minorities
Minority group
A minority is a sociological group within a demographic. The demographic could be based on many factors from ethnicity, gender, wealth, power, etc. The term extends to numerous situations, and civilizations within history, despite the misnomer of minorities associated with a numerical statistic...
into the value system
Value system
A value system is a set of consistent ethic values and measures used for the purpose of ethical or ideological integrity. A well defined value system is a moral code.-Personal and communal:...
of the dominant culture. Schrepp describes several applications of inductive ITA in the analysis of dependencies between items of social science questionnaires.
Example of an application
To show the possibilities of an analysis of a data set by ITA we analyse the statements of question 4 of the International Social Science Survey Programme (ISSSP) for the year 1995 by inductive and classical ITA.The ISSSP is a continuing annual program of cross-national collaboration on surveys covering important topics for social science research. The program conducts each year one survey with comparable questions in each of the participating nations. The theme of the 1995 survey was national identity
National identity
National identity is the person's identity and sense of belonging to one state or to one nation, a feeling one shares with a group of people, regardless of one's citizenship status....
. We analyze the results for question 4 for the data set of Western Germany
Western Germany
The geographic term Western Germany is used to describe a region in the west of Germany. The exact area defined by the term is not constant, but it usually includes, but does not have the borders of, North Rhine-Westphalia and Hesse...
.
The statement for question 4 was:
Some people say the following things are important for being truly German. Others say they are not important. How important do you think each of the following is:
1. to have been born in Germany
2. to have German citizenship
3. to have lived in Germany for most of one’s life
4. to be able to speak German
5. to be a Christian
6. to respect Germany’s political institutions
7. to feel German
The subjects had the response possibilities Very important, Important, Not very important, Not important at all, and Can’t choose to answer the statements.
To apply ITA to this data set we changed the answer categories.
Very important and Important are coded as 1. Not very important and Not important at all are coded as 0. Can’t choose was handled as missing data.
The following figure shows the resulting quasi-orders
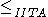from inductive ITA and 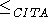from classical ITA.