Irregularity of distributions
Encyclopedia
The irregularity of distributions problem, stated first by Hugo Steinhaus
, is a numerical problem with a surprising result. The problem is to find N numbers, , all between 0 and 1, for which the following conditions hold:
, all between 0 and 1, for which the following conditions hold:
Mathematically, we are looking for a sequence of real number
s
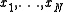
such that for every n ∈ {1, ..., N} and every k ∈ {1, ..., n} there is some i ∈ {1, ..., n} such that
Hugo Steinhaus
Władysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
, is a numerical problem with a surprising result. The problem is to find N numbers,
 , all between 0 and 1, for which the following conditions hold:
, all between 0 and 1, for which the following conditions hold:- The first two numbers must be in different halves (one less than 1/2, one greater than 1/2).
- The first 3 numbers must be in different thirds (one less than 1/3, one between 1/3 and 2/3, one greater than 2/3).
- The first 4 numbers must be in different fourths.
- The first 5 numbers must be in different fifths.
- etc.
Mathematically, we are looking for a sequence of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
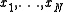
such that for every n ∈ {1, ..., N} and every k ∈ {1, ..., n} there is some i ∈ {1, ..., n} such that
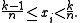
Solution
The surprising result is that there is a solution up to N = 17, but starting at N = 18 and above it is impossible. A possible solution for N ≤ 17 is shown diagrammatically on the right; numerically it is as follows:-
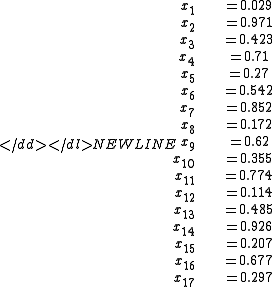
In this example, considering for instance the first 5 numbers, we have
-